Einstein e i suoi auguri
(versione originale italiana di Einstein is asked about dark matter – 4 gennaio 2019)
L/upd: 2019/05/26
Il grande Einstein ritorna e scherzosamente cerca di dare una soluzione relativistica, col suo caratteristico modo di ragionare, a problemi quali la rotazione delle galassie, il redshift misurato delle stelle e l’apparente bisogno di materia oscura. Lo fa, nella misura in cui è possibile, sforzandosi di usare un linguaggio umile e allegro, perché comprendere l’Universo è, secondo Einstein, semplice e meraviglioso.
Mi hanno raccontato ieri un fatto davvero singolare. Un gruppo di fisici teorici ha festeggiato questo capodanno insieme, e, dopo la mezzanotte e gli auguri, mentre chiacchieravano sulle varie ipotesi e idee in merito alla materia oscura e sullo stato del progresso della fisica teorica nella comprensione dell’Universo, si sono voltati tutti perché all’improvviso si sono accorti che sulla poltrona all’angolo stava seduto niente di meno che il grande Albert Einstein. Ovviamente si sono meravigliati moltissimo, sapendolo morto da quasi 64 anni..! Ma non hanno potuto fare a meno di considerare quella presenza un onore così raro da chiedere quasi subito proprio a lui cosa ne pensasse della faccenda della rotazione delle galassie e della materia oscura, visto che al suo tempo non era conosciuta questa problematica.
Il seguito è il resoconto della sua risposta.
“Prima di rispondervi in merito, colleghi, visto che da morto ho avuto molto tempo per pensare un po’ su tutto, vi propongo un gioco mentale. Seguitemi e poi vediamo se alla fine mi rifarete questa interessante domanda allo stesso modo.”
“Consideriamo una stella molto esterna e prossima al bordo galattico, che sta attualmente partecipando al moto di rotazione della nostra Via Lattea a circa 250 km/s. Sappiamo che, in base alla massa totale della materia visibile ed ordinaria che compone la nostra galassia, dovrebbe compiere questa rivoluzione a non più di 50 km/s. Ora supponiamo per assurdo, proprio per gioco, che per la componente di differenza, 200 km/s, sia lo spaziotempo stesso che stia ruotando a quella velocità in quella zona della galassia.
D’altronde, abbiamo capito che lo spaziotempo si può espandere, si può curvare, si può torcere.. proviamo a fare quindi il gioco mentale che possa possedere uno spin. Ovviamente non parlo di fenomeni relativistici estremi o quantistici come l’ergosfera o cose del genere, ma proprio di un nuovo tipo di rotazione classicamente intesa. Lo so che avrete pensato immediatamente: “e che ne è del redshift con cui misuriamo la velocità relativa della stella, se è lo spazio stesso a correre via?” Abbiate pazienza.. il nostro è un gioco pieno di sorprese!
Soltanto ricordate che fino ai tempi di Copernico, per spiegare il moto in cielo dei cinque pianeti conosciuti, e soprattutto la componente retrograda di questo moto, visibile per lunghi periodi, si ricorreva agli epicicli di Tolomeo, sfere che giravano su sfere fino a diversi ordini di complessità. Poi Copernico ipotizzò un unico movimento, la rivoluzione della Terra attorno al Sole, e la necessità degli epicicli scomparve: si scoprì che di essi si aveva solo un apparente bisogno, il quale durò finché non si fu disposti ad ammettere quell’unica componente imprevista (e finché non si fu disposti a rinunciare ad una certezza sino ad allora indiscussa, cioè che la Terra fosse il centro dell’Universo).”
“Ma come potremmo raffigurarci meglio una rotazione dello spazio? Prendiamo l’esempio della ruota girante del luna park, del tipo orizzontale, e in cui i seggiolini possono oscillare solamente in senso radiale. Sappiamo bene come si comportano i seggiolini e le persone che ci stanno sedute sopra mentre la ruota gira. Ma adesso è lo spazio che gira, non la ruota; come possiamo immaginare la situazione equivalente?
Forse è un po’ come se dovessi rincorrere una ruota girante attaccandoci di continuo i seggiolini! Così, proviamo ad attaccare, cercando di riuscirci, almeno un seggiolino ad una ruota che gira di già: siccome ogni possibile oscillazione è puramente radiale, vediamo subito che l’inerzia del seggiolino lo fa oscillare verso l’interno della ruota per un po’ di tempo, cioè la sua inerzia si comporta inizialmente in maniera centripeta. Ma se il seggiolino è riattaccato di continuo alla ruota, chiunque si trovasse sul seggiolino avrebbe questa impressione in maniera costante. E’ forse per questo che se è lo spazio a ruotare la stella non fugge via dalla nostra galassia? Dovremmo presupporre che uno spazio rotante acquisisca un potenziale inerziale il cui punto più basso è il centro di rotazione? Ci torneremo. Vediamo intanto che caratteristiche dovrebbe avere questo presunto potenziale inerziale, per combinarsi con una possibile e argomentabile rotazione dello spazio.
Immaginiamo sempre una ruota girante orizzontale questa volta delle dimensioni della ruota di un bus, ma sottile e fatta di piombo; sulla faccia superiore, lungo uno dei raggi, ci sono una serie di maniglie a distanza regolare. Se voglio bloccare la ruota quale maniglia sceglierò per evitare di slogarmi il polso? Ovviamente quella più esterna, perché anche se so che a mano a mano quelle più interne stanno girando più lentamente, capisco però che l’inerzia di tutta la parte di ruota che sta all’esterno di ogni maniglia gioca contro di me: per cui scelgo senza dubbio la maniglia più esterna. Proviamo quindi ad equilibrare queste due componenti, inerzia del seggiolino oppure del polso e inerzia della ruota.
Se torniamo alla ruota girante grande, quella coi seggiolini, con la variante della possibilità di attaccare i seggiolini in un qualsiasi punto dei raggi della ruota, e ci mettiamo in testa di voler fare sperimentare a tutti i seggiolini (e quindi a tutti quelli che ci stanno sopra) la stessa medesima trazione verso il centro nel momento in cui vengono agganciati in un qualsiasi punto del raggio, ebbene.. scopriremmo che ciò non ci è possibile con una ruota fisica: la decrescita lineare della velocità di rotazione non compensa la crescita quadratica dell’inerzia esterna al punto di attacco mano a mano che ci si sposta verso il centro. Ora, se facciamo l’ipotesi che la rotazione dello spazio attorno al centro della galassia invece stia facendo proprio questo, stia cioè imponendo la medesima “trazione” ad ogni punto del disco galattico, proporzionata alla densità di massa di un intorno di quel punto, dovremmo concludere che questa rotazione dello spazio decresca più che linearmente muovendosi verso il centro (ovvero cresca più che linearmente muovendosi verso il bordo) e che non si comporti quindi come la rotazione di una ruota materiale.
Ora, ogni raggio della grande ruota si sta comportando come una leva che ha sempre meno effetto positivo mano a mano che ci si sposta verso il bordo; anche se è difficile immaginare qualcosa di simile ad un effetto leva circa le stelle, ciò che conta di certo per noi (e per la continuazione del nostro gioco) è questo: se componiamo questa strana curva inerziale di rotazione con quella che deriviamo (dalle masse gravitazionali in gioco) come la curva di rotazione attesa, come risultato questa somma restituisce il moto delle stelle nella Via Lattea, in accordo con i dati osservativi, meglio che aggiungendo qualsiasi distribuzione di densità di materia oscura che siamo in grado di immaginare.
Ma a che cosa questa “trazione” costante che abbiamo introdotto potrebbe opporsi? Spostiamoci verso un’altra tappa del nostro gioco mentale.”
“Supponiamo adesso di essere in otto e di volerci attaccare ad una grande ruota girante che si trovi nello spazio profondo e a cui siamo vicini, proprio sopra, in condizione di assenza di gravità. La faccia che noi vediamo di questa ruota ha otto maniglie girevoli sul suo bordo esterno. Prima di attaccarci la ruota gira per inerzia.. e siccome non la vogliamo sbilanciare, scegliamo di afferrare ciascuno una maniglia, tutti nello stesso istante. Dopo un po’ di assestamento, se le maniglie possono ruotare senza attrito, avremo scoperto di avere tolto spin alla grande ruota, e di averne acquisito, ma in senso inverso, noi. Se non ci saremo messi come nei canotti, i grassi di fronte ai grassi e i magri di fronte ai magri, avremo sbilanciato lo stesso la ruota.. ma siamo bravi e ci abbiamo pensato prima.
Adesso ruotiamo attorno alla maniglia che ciascuno tiene in mano. Prima eravamo in assenza di gravità, in caduta libera, e ci sentivamo senza peso (e non sentivamo la nostra inerzia); adesso che peso sperimentiamo? Il contrario di un peso in effetti! Infatti sperimentiamo la forza che ci è necessario usare per rimanere attaccati alla maniglia.
Scegliamo di definire “inerzia propria” questa grandezza negativa (questo peso sotto lo zero) che ognuno di noi otto sperimenta. Siamo così giunti ad un nuovo step del nostro gioco mentale, quello in cui supponiamo che la rotazione dello spazio nella Via Lattea stia proprio applicando quella “trazione” che bilancia il suo opposto, cioè ciò che abbiamo appena chiamato inerzia propria. (E potete vedere che questo è esattamente il contrario di quello che sta facendo la grande ruota nello spazio profondo con ogni astronauta, al quale essa dà, aggiunge, inerzia propria, cambiando la sua condizione iniziale di caduta libera). Di conseguenza noi chiameremo, se siete d’accordo, “inerzia remota” la grandezza positiva che abbiamo chiamato “trazione” finora. Quindi, ruotando, tutto il resto della massa galattica sta aggiungendo inerzia remota ad ogni punto del disco galattico, in proporzione alla densità di massa racchiusa nel volume all’intorno di quel punto: tutto sta così bilanciando l’inerzia propria di quell’intorno. Bilanciando e quindi sottraendo l’inerzia propria, l’inerzia remota permette ad ogni corpo massivo di continuare la propria caduta libera gravitazionale (senza “sentire” né il suo stesso peso, né la sua stessa inerzia propria mentre lo fa).”
“Immaginiamo ora che, al posto della nostra stella esterna che ruota attorno al centro galattico, vi sia un candidato buco nero caratterizzato come segue: una massa alcune volte la massa solare, e fatto di oggetti equamente distanziati in un volume sferico; ogni oggetto non è altro che un piccolo buco nero primordiale, con la massa del Monte Everest e la dimensione di pochi nanometri. Poiché tutti questi oggetti sono così piccoli che fino alla fine del comune collasso gravitazionale qualsiasi collisione è molto improbabile, possiamo seguire la deviazione delle geodetiche (attraversate da quei corpi) durante una caduta libera continua [vedi Nota 1]. Dal punto di vista remoto, cioè il centro di rotazione non rotante della galassia, osserviamo l’inerzia propria del candidato buco nero bilanciata dalla sua inerzia remota (centripeta, a causa della rotazione dello spazio). Per ottenere invece il punto di vista fast-ticking [vedi Nt 2], dato che dobbiamo immaginarlo né accelerato né rotante, assumiamo l’equivalente della condizione in cui il singolo astronauta (il candidato buco nero) ha assorbito e centrato su di sé tutto lo spin della ruota ( lo spazio galattico tra il candidato e il punto f.t. stesso) nel senso opposto (come vediamo l’astronauta fare). Quindi, dal punto fast-ticking osserviamo i nostri mini buchi neri convergere gravitazionalmente, ma alla condizione di applicare alla deviazione delle loro geodetiche, nello stesso tempo, una componente di rotazione inversa (rotazione il cui asse è ortogonale al piano galattico). Di conseguenza, le deviazioni in un sistema inversamente rotante avranno la caratteristica di far convergere le singole accelerazioni di ciascun oggetto o mini buco nero verso una superficie sferoidale il cui raggio minimo polare è il raggio di Schwarzschild [vedi Nt 3] del candidato buco nero. Infatti, la componente centrifuga radiale dovuta all’inerzia è sempre uguale (secondo la nostra definizione di rotazione spaziale, supposta prima, una caratteristica ora estesa al corpo dell’astronauta) lungo il raggio del candidato b.n., e quindi avrà un’influenza proporzionalmente maggiore sulle accelerazioni minori, quelle degli oggetti posizionati più centralmente: così tutte le geodetiche convergeranno verso il percorso relativo più breve (quello che massimizza il tempo proprio) giusto adagiandosi su quella superficie sferoidale, dove ogni mini b.n. approssima ma non raggiunge mai la velocità della luce.
Dal punto di vista fast-ticking, sopra quella superficie sia l’inerzia remota combinata che le reciproche inerzie proprie degli oggetti non solo sono bilanciate, ma anche minimizzate, fino a un livello di inerzia propria combinata uguale a quello dell’intero candidato (il perno della maniglia), se misurato dal punto remoto (il centro di rotazione galattico). Interessante, non è vero?”
“D’altra parte, notiamo un fatto molto significativo in relazione a ciò di cui stiamo parlando. Nel bulge galattico la massima densità di gas e la linea massima di formazione di nuove stelle vengono raggiunte in un’area appena fuori, ma molto vicina al raggio di Schwarzschild galattico, così come siamo in grado di calcolarlo secondo la stima attuale della massa della galassia. Più all’interno, da quella zona al corpo supermassivo centrale, la densità delle particelle precipita improvvisamente e in un modo davvero inspiegabile, se non si tiene conto che la gravità e la riduzione al minimo dell’inerzia propria della materia la fanno convergere con la sua massima densità verso quella superficie sferoidale (che non è altro che la dilatazione relativistico-inerziale del centro di massa galattico come era inteso nella teoria della gravità newtoniana).
Continue oscillazioni, al di sopra e al di sotto (o al di fuori e al di dentro) di quella superficie ideale fanno sì comunque che della materia (gas o corpi stellari) si trovi al di là, cioè più all’interno. Mentre nel caso precedente, quello del buco nero stellare, la materia collima verso l’esterno perché riguadagna inerzia propria (subisce un deficit di inerzia remota), al di là del centro di massa galattico la materia è costretta invece a collimare verso l’interno per fare la stessa cosa, ed ogni geodetica può solo terminare nel b.n. supermassivo centrale: infatti in quella zona la rotazione dello spazio assume un altro senso, che potremmo chiamare time-verse [vedi Nt 4].
A pensarci bene dovrei dire che ciò è una fortuna, perché è soltanto l’inevitabile esistenza di questa zona cuscinetto al centro delle galassie che non ha reso l’Universo omogeneo a qualsiasi scala, ma solo a scale molto più grandi di quelle galattiche. Questo sin da un’epoca molto remota in cui lo spazio non aveva ancora avuto il tempo di dispiegare completamente i suoi spin. Infatti, se lo spin dello spazio fosse stato trasmesso istantaneamente, non avremmo avuto i b.n. centrali supermassivi, frutto di un momentaneo eccesso locale di spin (Cioè, siamo nella situazione in cui l’astronauta ha appena afferrato la maniglia ed il suo polso sostiene una eccessiva torsione ed una eccessiva accelerazione rispetto a quelle finali, quindi quando l’eccesso di torsione è passato oltre, quel momentaneo surplus di accelerazione – prima che l’astronauta sia finalmente diritto e disteso – ha condannato una parte della materia ad essere , prima o poi, confinata nel corpo compatto centrale ed in uno spazio rotante in senso time-verse [vedi sempre Nt 4]: senza questo fenomeno nessuna zona cuscinetto e quindi nessuna rilevante mancanza locale di omogeneità).
Per quanto riguarda il b.n. supermassivo centrale in sé, beh, notiamo che in questo caso punto di vista remoto e p.d.v. proprio coincidono, quindi: il punto di vista immaginario fast-ticking, per mantenersi non rotante e non accelerato, continua a vedere la rotazione dello spazio al contrario, cioè come lo spin dell’astronauta piuttosto che come lo spin della ruota, e le nostre considerazioni sono le stesse che nel caso del buco nero di massa stellare (la materia ruota ad una velocità prossima a quella della luce, emettendo energia sotto forma di onde radio uniformemente distribuite); invece, dal suo punto di vista proprio, il b.n. centrale vede che la sua inerzia propria non è bilanciata da nulla, perché nulla che abbia una massa significativa sta spazio-ruotando attorno ad esso, vale a dire lungo il suo senso di rotazione time-verse [ancora Nt 4] (parimenti il suo spazio non ruota attorno ad alcun punto remoto – come la grande ruota nello spazio profondo, la cui rotazione non ha perno). Di conseguenza non può fare altro che trascinarci nella sua caduta libera inerziale, quella che ci fa allontanare da quasi tutte le altre galassie dell’Universo.”
“A questo punto, lasciatemi dire che – se il nostro gioco mentale vuole avere un senso! – allora dovremmo affermare che ogni massa, piccola o grande (la stella al bordo della galassia, i mini buchi neri, il buco nero stellare, il buco nero supermassivo, un pianeta, un asteroide, un protone, ecc.) possiede tanta inerzia propria, quanta le sue componenti (che ne hanno fatto nel tempo un oggetto gravitazionalmente legato) ne hanno inversamente conferita a tutto il resto della materia dell’Universo nel passato, attraverso lo spin che hanno localmente impresso allo spazio, co-generando così la contro-componente globale, o inerzia remota. Pertanto, la composizione universale di queste due quantità è zero, in ogni epoca.
Se tutto ciò descrive correttamente l’aspetto inerziale della massa, la distribuzione omogenea e isotropa della materia nell’Universo soddisfa la logica probabilistica di mantenere l’inerzia remota universale ad un livello minimo, dal punto di vista di un qualsiasi osservatore in un qualsiasi tempo: il nostro è semplicemente l’universo più probabile che potrebbe capitarci di osservare. Se le galassie, o meglio gli ammassi di galassie, non compongono positivamente i rispettivi spin, si allontanano fra loro in caduta libera inerziale, cioè, ciascuno da tutti gli altri verso il punto con il potenziale gravitazionale più alto (che è anche quello con il potenziale inerziale più basso), perché mentre guadagnano questa accelerazione compensano la loro inerzia propria (non sentono il loro proprio peso inerziale).
Le perturbazioni dei rispettivi spin formano i filamenti di galassie, i superammassi, ecc. La composizione di tutti gli spin universali è zero, cioè l’Universo non ruota e non ha inerzia; in questo senso, la descrizione relativistica dell’Universo è indipendente e rimane indipendente da qualsiasi esigenza di avere uno spazio o un tempo di riferimento assoluti, anche secondo le conclusioni del nostro gioco mentale.”
“Ma se è così, mi direte, che ne è del principio di equivalenza?
Bene, potremmo dire che l’abbiamo utilmente convertito in una proprietà emergente: ogni osservatore osserverà sempre localmente il principio di equivalenza, perché non può evitare di stare in uno spazio rotante o in una condizione di accelerazione (e soggetto a marea inerziale); quindi l’astronauta sulla Luna che lascia cadere il martello e la piuma, osserverà sempre il principio riprodotto, perché tutti e quattro i corpi, la Luna, l’astronauta, il martello e la piuma, subiscono un’interazione nel frattempo, proporzionale alla loro massa, da parte dell’inerzia remota di tutti gli altri corpi galattici, a causa della rotazione comune: inerzia che è esattamente inversa all’universale caratteristica centrifuga dell’inerzia propria dei quattro oggetti. Se portiamo la Luna, l’astronauta, il martello e la piuma tra due galassie in una condizione equipotenziale (cioè di supposta assenza di rotazione correlata allo spazio), il nostro satellite non potrà fare a meno di accelerare in caduta libera inerziale, nel mentre acquisterà gradualmente un crescente spin per una sorta di effetto di marea inerziale; cosicché queste due componenti faranno ancora avere successo al nostro esperimento, anche se nel senso opposto: col tempo, martello e piuma astronauta (e anche molta polvere e tanti massi) cominceranno ad allontanarsi dalla Luna, perché il nostro satellite non è strutturato affatto come una galassia (e ciò precisamente perché, all’interno di una galassia, ci è nato).
Quindi, a questo punto, dobbiamo concludere che la massa inerziale supera sempre, e in un modo non microscopico, la massa gravitazionale, ma non c’è osservatore che possa sperimentare ciò all’interno di un laboratorio.
Tutto questo fornisce anche una risposta all’obiezione iniziale circa l’effetto Doppler: se considero la nostra stella esterna, in relazione alla sua velocità differenziale (200 km/s), come trascinata dallo spazio, devo assumere di conseguenza un punto di vista in cui rimango indietro, e quindi mi faccio superare dallo spazio stesso; in altre parole, ho bisogno di mantenermi accelerato. Quindi, attribuire il redshift differenziale alla mia stessa velocità, o alla velocità della stella, o alla sua massa relativistica remoto-inerziale, o alla mia accelerazione inversa (cioè alla mia inerzia propria relativa), è, secondo il principio di equivalenza, affermare quattro cose equivalenti.”
“Grazie al nostro gioco mentale, e cioè passando dal trattamento dei sistemi uniformemente accelerati al trattamento dei sistemi spazio-rotanti, la mia Relatività diventa molto più completa (e anche più divertente). Nel tempo a venire, i seguenti quattro pilastri, vale a dire la considerazione dei sistemi spazio-rotanti, l’emergenza del principio di equivalenza, la differente concezione dell’orizzonte cosmologico e la proprietà emergente del tempo proprio (più utilmente trattato come misura esatta di una metrica speciale), costituiranno le basi per trasformare la mia teoria in una teoria della Relatività Universale.”
“Inoltre la Relatività, nella sua essenza, si profila probabilmente come una teoria Machiana [vedi Nt 5]; e, ci fossero voluti secoli, è questa la vera ragione della mia venuta oggi dall’oltretomba, e del mio discorso qui con voi: vedo la ragazza che sente le sue braccia alzarsi mentre guarda tutto il cielo e tutte le sue stelle che stanno girando insieme. Fate ciò che vi sembra meglio, è ovvio, anche se vi suggerisco ciò che l’imperatore Settimio Severo disse sul suo letto di morte: Laboremus!”
“Adesso se volete chiedermi ancora cosa ne penso della materia oscura bene, sennò offritemi qualcosa da bere..! Intanto auguri a voi.”
Redatto da Giorgio Mistenda.
Dedicato a Albert Einstein e a Roger Penrose.
English version: Einstein is asked about dark matter.
Prima stesura 2019/01/04. Releases italiane: 2019/01/07; 2019/01/04.
Note del redattore:
1) In Relatività Generale, la deviazione delle geodetiche è l’avvicinarsi o allontanarsi l’uno dall’altro degli oggetti mentre si muovono attraverso un campo gravitazionale, a causa del gradiente o differenza di intensità del campo stesso in punti diversi dello spazio. Così se due oggetti si stanno muovendo lungo due traiettorie parallele, la presenza di un gradiente gravitazionale di marea farà sì che le traiettorie si pieghino o verso o lontano l’una dall’altra, producendo un’accelerazione relativa tra i due oggetti. Vedi https://en.wikipedia.org/wiki/Geodesic_deviation e https://en.wikipedia.org/wiki/Tidal_force.
2) L’osservatore fast-ticking è, in Relatività Generale, l’osservatore inerziale, cioè non soggetto ad accelerazione, molto distante dal campo gravitazionale, e, nel nostro caso, posto in posizione polare, cioè non rotante; il suo orologio, constatando la relativa lentezza di tutti gli altri orologi, è fast-ticking, cioè con il ticchettio più veloce; in conseguenza di ciò, il suo è l’orologio che registra la maggior durata di un evento.
3) Il raggio di Schwarzschild è il raggio minimo teorico della sfera entro cui dovrebbe essere compressa tutta la massa di un corpo perché la velocità di fuga sulla sua superficie risulti pari o maggiore della velocità della luce; se il corpo procede nel suo collasso, il raggio di Schwarzschild rimane il raggio della sfera che ne delimita l’orizzonte degli eventi, poiché nessuna informazione può uscire dall’interno di quella sfera.
4) In questo caso infatti la rotazione dello spazio assume un aspetto “time-verse”. Per un’esposizione più dettagliata (e formale), consultare l’articolo da me dedicato: Il centro della galassia: una holostar.
5) Per il principio di Mach, relativo all’inerzia, vedere il Principio di Mach.
Vedere sotto l’appendice per i commenti.
********
APPENDICE:
bozze per dibattito e sviluppo futuro
L/upd: 2019/03/03
1. Mi sveglio (come nel film The Cube) dentro un enorme ascensore tondo di dimensioni galattiche (semplifichiamo elidendo tutti i moti normo/gravitazionali interni alla Via Lattea, i rapporti con le galassie dell’ammasso, il supercluster della Vergine, ecc). La prima cosa che noto, oltre il fatto che non trovo la macchinetta del caffè, è che non mi sento accelerato, non sento il mio peso. Siccome sarò un po’ stordito dal risveglio ma mi ricordo qualcosa di fisica, realizzo che ci sono solo tre possibilità: o sono fermo (?), o sono in moto rettilineo uniforme in una zona di spazio totalmente senza potenziale gravitazionale, o sono in caduta libera. Non conosco altre situazioni inerziali. Per distinguere le prime due dalla terza ho però una possibilità. Siccome se sono in caduta libera solo il centro di massa dell’ascensore è effettivamente in caduta libera, posso vedere se fra due zone molto periferiche dell’ascensore riesco a misurare fenomeni di marea (ovvero accelerazioni locali in senso opposto fra di loro – in questo caso ovviamente non normo/gravitazionali, cioè come se ci fosse un peso nei due sensi contrapposti). Se le misuro, allora cerco i due punti di massimo e il diametro che li collega è la mia direzione di moto istantanea. Se andasse davvero così, però succederebbe qualcosa di molto scioccante pure: avrei trovato la direzione ma non il senso, e capisco che non ci sarebbe nessun esperimento possibile da condurre all’interno dell’ascensore che mi permetta di individuare il senso della mia direzione di moto. Quindi saprei con certezza che mi sto spostando in caduta libera verso un centro di massa, conosco la direzione istantanea del mio moto, ma nello stesso tempo per me osservatore il vero centro di massa ed il punto diametralmente opposto nello spazio si comportano esattamente allo stesso modo. (Questo fenomeno deve farci riflettere sul rapporto inerzia/gravità: la mela non si sente accelerata, e dal suo punto di vista è la Terra che fa dei piccoli movimenti strani verso il suo centro di gravità; io dall’ascensore non ho modo di distinguere il verso perché non c’è differenza fisica fra muoversi verso un centro di massa e avvertire marealmente una cosa muoversi verso il proprio centro di massa; è anche per questo che continuo a parlare di caduta libera inerziale ad ogni scala che escluda l’universo intero). Comunque, alla fine io non trovo una accelerazione mareale con dei massimi in qualche punto privilegiato, ma trovo una accelerazione periferica diffusa e tangente (un eccesso di rotazione). Ho due possibilità: o l’accelerazione diffusa e tangente è dovuta ad un elemento non considerato interno al mio sistema, oscuro e massivo, o sono in una caduta libera che non è diretta verso un centro di massa, ma che è diretta ad allontanarsi da tutti gli altri centri di massa (che sono mediamente distribuiti uniformemente, oltre una certa scala). Mi affaccio da un oblò anche per svegliarmi un po’ e vedo il redshift globale degli altri ascensori. Di nuovo non ho che le stesse due possibilità: o è l’espansione dello spazio (causata da un elemento oscuro esterno a loro tutti) che causa il redshift, tutti gli ascensori sono in moto rettilineo uniforme o fermi (?), e l’accelerazione tangenziale non è marea ma è dovuta ad un elemento interno ad ognuno, massivo ed oscuro; oppure posso pensare che gli altri ascensori sono combinati esattamente come il mio, che tutti gli ascensori si stanno allontanando fra di loro con una accelerazione uniforme (in caduta libera inerziale) e quindi che tutti stanno sperimentando il mio stesso tipo di marea senza una direzione privilegiata.
2. Tutta la relatività generale si poggia su questo assunto. Il corpo in caduta libera segue il percorso più breve, che è la curva spazio-temporale o geodetica che massimizza il tempo proprio. La deviazione in un senso qualsiasi dalla geodetica può avvenire solo se il corpo subisce una ulteriore forza, sempre in un senso qualsiasi, e ciò gli fa avvertire il proprio peso (che è la reazione inerziale opposta e contraria alla forza che subisce). La forza che avverte è quella richiesta per fargli fare un percorso spazio-temporalmente più lungo. Come si diceva, mentre sto qui seduto a scrivere sono in una caduta libera ostacolata dalla sedia prima e dal pavimento poi. Entrambi, io ed il pavimento, quindi, sentiamo, in direzione opposta, il mio peso. La mia caduta libera, in conseguenza di queste forze, è rinviata (in questo caso, semplificando, solo nel tempo) e quindi allungata. Quando l’operaio cadde dal tetto disse ad Einstein di non aver avvertito il proprio peso, mentre cadeva. Ovviamente finché non ha sbattuto, cioè finché il suolo non ha bloccato la sua caduta libera. E allora il suo peso l’ha sentito sì (ed anche il suolo).
3. Volevo solo aggiungere un’osservazione riguardo ai 120 ordini di grandezza in più (un numero con 120 zeri) fra l’energia del vuoto e la costante cosmologica richiesta dal modello corrente. Questo dimostra che si deve evitare il riduzionismo. L’energia del vuoto, in QM (da ora in poi, Meccanica Quantistica), è il “metodo” che ha il vuoto per mantenersi indifferente al background. Estendere questa logica allo spazio globale, cioè al background stesso, equivale ad “insegnare” al background come essere indifferente a se stesso: infatti lo fa subito, espandendosi così velocemente da esaurire la vita dell’Universo in pochi secondi. Più indifferente di così! Insomma, ogni teoria ha il suo ambito, e non uso i modelli meteo per capire perché in certi orari i bambini affollano le scuole e in altri no, anche se questo non esclude completamente interferenze (per ora a senso unico, nel senso che il meteo può, in casi estremi, condizionare il comportamento dei bambini, ma non succede l’inverso).
Caro Giorgio, grazie per questo spazio che hai messo a disposizione per ragionare sulla tua proposta.
Da non-cosmologo, mi limito a semplici annotazioni sulle implicazioni che vedo in questo modello.
1. la materia su grande scala ha una distribuzione uniforme.
2. esiste una forza repulsiva che fa aumentare progressivamente le distanze tra una galassia e tutte le altre con moto accelerato ad accelerazione costante.
3. l’accelerazione costante implica una crescita progressiva della velocità di allontanamento.
4. esiste necessariamente un fattore limitante che impedisce che questa velocità superi la velocità della luce. In altri termini deve esistere un momento in cui l’accelerazione si riduce a zero.
5. lo spazio non si crea , non si estende, ma preesiste e viene occupato sempre più dalle galassie in movimento.
6. regredendo nel tempo vediamo che tutte le galassie confluiscono in uno spazio sempre più ristretto fino ad un punto in cui tutta la materia era inizialmente concentrata.
7 .procedendo in avanti nel tempo il processo di diluizione delle galassie nello spazio prosegue indefinitamente, secondo un modello di universo in espansione in cui tutte le galassie sono destinate ad allontanarsi reciprocamente , senza però superare la velocità della luce.
Ora mi chiedo se queste implicazioni sono coerenti con il modello che proponi o sono fuorvianti e vanno riformulate in altro modo.
Mi chiedo anche quali osservazioni potrebbero trovare riscontro in questo schema, ossia esistono conseguenze verificabili che il modello è in grado di predire? Non sarebbe una condizione sufficiente per poter affermare che il modello rappresenta la realtà fisica, ossia le cause, ma sarebbe comunque un modo efficace per descriverne gli effetti.
LikeLiked by 1 person
Nel commento precedente (ero loggato in WP) non mi sono presentato, anche se forse avrai riconosciuto il mio avatar, il medesimo che uso nell’infinito Teatro del Cosmo.
Il mio nome è Maurizio, puoi leggere il mio profilo nel blog, come già detto, non ho un background che mi consenta di portare un contributo qualificato alla discussione, ma mi auguro che in qualche modo, anche un commento banale, possa esserti utile.
LikeLiked by 1 person
ciao Maurizio, grazie del tuo contributo!
Comincio dalla fine. Ogni teoria si basa, sia come sua genesi nella nostra mente, sia come possibilità di esame, su l’osservazione di fenomeni non completamente spiegati da teorie precedenti. In genere, per essere consistente, deve spiegare tutto quello che le precedenti spiegavano bene, più qualcosa. Le teorie precedenti diventano così casi speciali della teoria nuova, che è un po’ più generale. In questo caso il problema di partenza era l’apparente necessità di aggiungere materia oscura, e in proporzione molto rilevante (5/6 volte tanto la materia “normale”), perché la nostra teoria della gravità, la GR, spiegasse bene i moti di rotazione delle galassie (e non solo, anche quelli delle galassie satelliti, degli ammassi di galassie ecc.). Ci sono stati e ci sono senza fine quelli che cercano di correggere la GR, ma i risultati sono sempre peggiorativi, sotto un qualche aspetto o a qualche scala. Inoltre, anche non volendo escludere ovviamente la scoperta di particelle nuove (ma ti ricordo che l’ LHC continua a fare esperimenti a crescenti energie, ma non trova niente da ben 6 anni), la distribuzione che eventualmente dovrebbe avere questa materia oscura, per render conto della reale rotazione delle stelle della galassia, è a dir poco assurda, perché non dovrebbe concentrarsi al centro né essere casuale, ma mantenersi a dovuta distanza e un po’ a ciambella. Ora, una galassia medio/grande come la nostra ha conosciuto, nell’arco della vita dell’universo, almeno 100 fusioni con altre galassie: come può essere mai pensabile che questo grande salvagente di materia oscura si sia mantenuto in quella configurazione? Quindi, se una teoria sbroglia in modo semplice questa faccenda, ha poco bisogno di essere predittiva. Comunque la mia idea contiene un potente elemento predittivo (fin troppo). Per una serie di considerazioni (su cui sto scrivendo qualcosa in questi giorni) non prevede singolarità gravitazionali. Mi devo pure sbrigare, perché gli scienziati che stanno usando la VLBI hanno annunciato nuovi risultati entro primavera, mentre quelli che ci hanno già dato sono davvero strani: parliamo di Sagittarius A*, il grande buco nero centrale della nostra galassia; mentre tutti si aspettavano un grande disco scuro con attorno le sfavillanti emissioni radio (getti di materia che in parte riesce a sfuggire dai poli a velocità prossime a quelle della luce) abbiamo trovato come un leggero getto puntato proprio verso di noi, come se quel bestione ci stesse facendo l’occhiolino. E’ come se Galileo avesse puntato il suo cannocchiale verso la luna, e, appena fatto, vede un “lunare” che sta puntando a sua volta il cannocchiale verso di lui. Ho provato a segnalare questa loro conclusione come assurda: innanzitutto Sgr A* dovrebbe ruotare come Urano, cioè coricato, diciamo, rispetto al disco galattico.. poi avere il polo puntato esattamente verso di noi, che è come vincere al superenalotto tutte le settimane per un lustro di seguito. Ma poi, materia lanciata verso di noi a velocità prossima a quella della luce.. quanto blueshift dovrebbe avere? Per questo ho una certa confidenza che stiamo vedendo probabilmente proprio lui, e non un getto di materia. Ecco il link dell’articolo e le loro conclusioni, così puoi vedere anche tu le immagini: https://www.media.inaf.it/2019/01/22/sagittarius-a-star-alma/
La semplicità e la predittività di una teoria consiste però anche nel fatto che ci risultare inutili altre variabili ad hoc del nostro modello cosmologico, senza essere nata per fare questo.Quanto poi all’essenza, è totalmente la GR, estesa ad un nuovo modo di concepire l’inerzia, distinguendola in propria (dell’osservatore o di un corpo) e remota (quella degli altri corpi di un sistema, come una galassia). Mentre l’energia della massa gravitazionale scala (cioè sommata dà zero) con la curvatura (pensabile come estesa all’infinito – lo spazio di quella massa), l’energia della massa inerziale propria scala (dopo meccanismi di compensazione intragalattici e intraammassivi dovuti appunto allo spin) con l’inerzia remota del resto dell’universo. Da una parte questo ha causato lo spin spaziale delle galassie fin dalla loro nascita, dall’altra la massa inerziale remota dell’universo non può conoscere sottrazioni, perché nulla può superare la velocità della luce, e come non può andarsene l’osservatore, così non può lasciare il campo qualcosa della sua controparte. Quindi la massa inerziale dipende dal tempo cosmologico, cioè da quanto i rispettivi osservatori vedano il rispettivo redshift dovuto alla massa relativistica, piuttosto che alla velocità. Ed in definitiva essa corrisponde alla somma sia di energia oscura sia di materia oscura (per quella parte necessitata dal modello corrente al di fuori del nostro ammasso), la massa mancante alla densità critica, insomma. La componente massa relativistica c’è sempre stata (niente nell’universo è mai stato fermo) ed un corpo accelerato, se non può essere visto accrescere la sua velocità relativa, sarà visto accrescere la sua inerzia relativa remota. L’inerzia relativa si comporta come una antigravità (dal punto di vista di un osservatore), senza mettere in campo alcuna forza, senza cambiare natura alla caduta libera di tutti i corpi dell’universo, e quindi senza alterare in nessun modo l’emergenza del principio di equivalenza. Come viene preservata la caduta libera e l’emergenza del principio? Estendendo la GR dai sistemi uniformemente accelerati ai sistemi spazio-rotanti. E torniamo lì da dove eravamo partiti!
E’ chiaro che andremo chiarendo sempre meglio i vari punti. Però tieni a mente questa osservazione: a differenza della massa gravitazionale, la componente relativistico/inerziale della massa è relativa: se acceleriamo un protone nell’ LHC fino a velocità prossime a quelle della luce, tutta l’accelerazione che diamo in più si converte in massa inerziale. Dal punto di vista del protone, però, è l’acceleratore che sta girando all’inverso a velocità prossime a quelle della luce, ed è sempre quest’ultimo che sta accrescendo la propria massa.
LikeLike
Quanto allo spazio che preesiste, ecc., non vedo perché questo modello dovrebbe vederla così. Lo spazio è il campo gravitazionale/inerziale dell’universo. Dal mio punto di vista in questo caso le conclusioni sono provvisorie, ma il modello della EGR è completo (almeno concettualmente), cioè non spiega e non gli è richiesto di spiegare niente di meno o niente di più di quello attuale a proposito della natura dello spazio (e del tempo). Dico solo che per una completa comprensione dell’intero fenomeno cosmologico (come visto da un osservatore sia proprio che remoto) è necessaria una considerazione più fine del tempo proprio e del concetto di orizzonte cosmologico, cosa che mi riprometto di fare nel futuro. Ma non manca niente, parlando di spazio, rispetto al modello attuale. Le galassie sono in caduta libera gradualmente decomposta fra di loro e netta dal rispettivo background. La relazione con il loro spazio locale, che per altri aspetti è importante o decisiva, è indifferente invece da questo punto di vista, perché nessuno spazio locale è periferico rispetto all’universo. Cioè, è lo spazio inteso come background che si comporta, per ogni singolo osservatore, come preesistente, non lo spazio locale. E questo vale anche per una galassia remotissima, che ci vede invece nel suo background. Ognuno vede l’inerzia remota come causa della propria caduta libera, e questo è anche logico, visto che ognuno si sente osservatore e non osservato, e soprattutto non si vede periferico. Ma ciò non implica la preesistenza a livello globale dello spazio. Implica soltanto che non si può avere un punto di vista diverso da quello di un osservatore concreto.
Per ora mettiamola così: l’approssimazione ad una relatività universale (che come detto dovrà occuparsi prima di tutto del concetto di tempo) si può fare dando alla faccenda dell’espansione due direzioni, entrambe provvisoriamente efficaci, di cui una appare convenzionalmente preferita.
Quando diciamo che l’inerzia remota si comporta come una antigravità, non diciamo che è in gioco un principio repulsivo, poiché non è in gioco nessuna forza, ed il fenomeno è solamente interpretativo. Se vediamo la luce di una stella passare vicino alla massa del sole, la massa relativistica fa il suo lavoro esattamente come previsto. Ma io non sto guardando a quel fotone deviato allo stesso modo in cui guardo alla inerzia remota del mio background, perché in questo secondo caso devo tenere conto che sto guardando pure l’inverso della mia inerzia propria. Cioè: è la mia massa inerziale propria che ha il segno meno (per convenzione), come quella gravitazionale ha invece il segno più; così, sempre per convenzione, l’inerzia remota ha segno più (cioè lo stesso segno della massa relativistica del fotone deviato dalla massa solare) come il potenziale gravitazionale ha il segno meno. Quindi in un certo senso sono io osservatore che mi comporto come antigrave, conservando tenacemente la mia condizione di caduta libera; è la nostra galassia che resiste pervicacemente in questo verso, perché non c’è nessuna forza a cui ricorrere per rallentarla. Però, come per quel diametro tracciato nell’ascensore galattico, non avendo modo di distinguere il senso della nostra caduta libera, scegliamo la convenzione di dare lo stesso segno di quelli dati comunemente, per comodità, consuetudine, e forse migliore possibilità di rappresentazione. In senso stretto, anche se la direzione dell’espansione dell’universo fosse contraria, cioè le galassie stessero tutte collassando (in caduta libera), ciò non toglie che fra di loro si vedrebbero allontanarsi, nella misura in cui starebbero deviando assieme alle loro geodetiche (nello spaziotempo). Siccome noi tutti abbiamo visto solo un tratto breve della vita dell’universo, non è detto che sapremmo distinguere le due situazioni, come non sappiamo distinguere il senso di moto da dentro l’ascensore (e neanche guardando dall’oblò). Quindi scegliamo i segni secondo la cosa che ci viene meglio pensare, giustamente. Eppure in questo secondo caso, così difficile da raffigurarsi, vedendo che la gravità sta facendo il suo lavoro, quello che mi aspetto che faccia, a nessuno verrebbe in mente il problema della preesistenza dello spazio. Perciò: una interpretazione facilmente rappresentabile, l’espansione, pone problemi di preesistenza dello spazio in cui effettuare la caduta libera; una interpretazione difficilmente rappresentabile, il collasso, però ci semplificherebbe la vita come se ci offrisse spazio a volontà.
Comunque stringendo la situazione si può rappresentare così: da un punto di vista remoto lo spazio si comporta come preesistente, cioè come background relativamente dato per ognuno che osservi; da un punto di vista proprio nessuno si vede periferico. Poiché questo vale per ogni possibile osservatore, e ciascuno è anche alternativamente background, lo spazio non è un sistema di riferimento assoluto ma relativo di cui non ha senso postulare la preesistenza, perché non è richiesta ad alcun fine, ed anche la non preesistenza, perché anche questo non ci aggiungerebbe alcun elemento (a questo stato della teoria e per i fini che si è ripromessa al momento).
LikeLike
Ripensando all’enorme ascensore “tondo” in caduta libera… esso si trova circondato da ogni parte da identiche strutture, che su esso esercitano ciascuna un effetto di marea, in modo tale che, alla fine non vi sia alcuna direzione privilegiata. Se vi fosse solo una coppia ad interagire avremmo una precisa deformazione che ci indicherebbe la direzione della congiungente i loro centri.
Questo non equivale a dire che la risultante “radiale” delle azioni mareali è nulla?
Se l’effetto mareale non è radiale, ma come affermi, si traduce in una accelerazione diffusa, periferica tangenziale, motore di una rotazione “extra” dell’ascensore (Galassia), il fatto che vi sia in atto un allontanamento reciproco non implica che l’effetto mareale ( proporzionale all’inverso del cubo della distanza) sia in progressiva attenuazione? In altri termini , non dovrebbe esserci un progressivo rallentamento di questo moto di rotazione “extra” ?
LikeLiked by 1 person
Ciao Mauri, grazie della domanda perché è calibratissima e più che opportuna, e perché ci darà l’opportunità di chiarire cosa si intende esattamente per background (dal nostro punto di vista relativistico). Ti risponderò perciò più che volentieri più tardi.
Nel frattempo ho capito che alcune incomprensioni derivano da una errata mia stesura di un concetto (relativo all’osservatore reale) nel mio ultimo articolo sulla marea, che in effetti non ho più rivisto dopo averlo scritto per L’Infinito Teatro. Francamente non mi ricordavo nemmeno di avere scritto qualcosa in merito, ma ieri, volendo rivedere l’articolo per linkarlo finalmente su Twitter e su FB, mi sono accorto del problema. E’ vero che il complicato rapporto fra galassia e buco nero centrale potrebbe condurre a quelle conclusioni, ma siccome il ragionamento sarebbe lunghissimo e scriverlo in inglese mi richiederebbe qualche mese, ho erroneamente lasciato lì la cosa come mi era venuta. Ho già rivisto l’articolo introducendo un concetto più calibrato ( https://giorgiomistenda.com/2019/02/26/local-space-tide/ ), aggiungerò qualcosina nel tardo pomeriggio per rendere quella parte meno asciutta, infine risponderò a questa tua decisiva domanda. Già da ora posso dirti che il rapporto locale/globale sembra sempre dettato da una logica di minimizzazione della massa relativistica (o inerzia relativa), dato un certo grado di entropia (età dell’universo). Marea ed espansione, spin e caduta libera, che a noi sembrano percorsi così problematici, sono piuttosto gli “ingranaggi” che consentono ai “componenti” il minor movimento possibile, in media, il minor “spreco” in movimento, mi si passi il termine, mentre l’entropia, ad ogni dato momento (e a questo stadio della nostra teoria) è un dato di fatto legato al tempo. La quantità di moto dell’intero universo è zero, per cui possono esistere soltanto movimenti relativi. Non pensare che la nozione comunemente accettata di energia oscura, introducendo un elemento immobile, ed a scarsissima densità, renda più comprensibile o più lampante la cosa di quello che vado dicendo io, perché ad un certo punto introduce moti che non sono più relativi, cioè zone dell’universo che si perdono di vista. Però proprio per questo sono decisive queste tue domande così anche io capisco come esporre meglio quello che penso. A dopo.
LikeLiked by 1 person
Allora, eccoci ai miei soliti orari impossibili. Intanto i moti inerziali non rallentano se non per qualche motivo (frizioni, attriti, o addirittura maree). Suppongo però che tu intendi “rallentamento dell’accelerazione” ed immagino intendi “col passare del tempo cosmologico”.
Intanto un po’ di fenomenologia: tutto sembra ruotare troppo. Dalla rotazione delle galassie siamo proprio partiti, quindi inutile dilungarci. Le galassie satelliti sembrano essere troppo poche per il modello standard, e soprattutto ruotare troppo (intorno al compagno più grande) perfino con l’aggiunta di materia oscura, perfino con la sovrastima della massa barionica degli aloni galattici. Le nubi di Magellano mostrano grandiosi effetti mareali, ma sono troppo veloci, sembrano passare per la prima volta nelle nostre vicinanze (il che complicherebbe la questione dello scarso numero di satelliti). Se lo spin spaziale della Via Lattea dominasse e inglobasse i suoi satelliti invece la faccenda si porrebbe allo stesso modo che per le stelle più esterne del disco. Non solo non serve materia oscura, ma probabilmente serve molta meno materia barionica negli aloni. Le strutture locali sono molto asimmetriche, se rapportiamo questa asimmetria alla loro scala. Non dimentichiamo che le grandi galassie a spirale sono simmetriche solo lungo due dimensioni, ma si allontanano enormemente dalla sfericità lungo la terza. Questo complica notevolmente e rende molto perturbativi i rapporti fra noi e la galassia di Andromeda, perché non condividiamo affatto lo stesso piano di rotazione (e quindi lo stesso asse). A sua volta i due semi gruppi (galassie più satelliti) MW e Andromeda mostrano una struttura a manubrio, con quella del Triangolo troppo grossetta per prendere posizione. Il nostro gruppo è molto periferico rispetto al superammasso della Vergine, il quale presenta importanti irregolarità di distribuzione della massa. Per non dire poi dei filamenti.
Ho fatto un po’ di fenomenologia così mi consentirai di partire da una situazione di fatto. Sia la rotazione eccessiva sia la notevole irregolarità ci sono. Nel primo articolo semplicemente cerco di spiegare perché le stelle non fuggono via nonostante questo innesto di inerzia. Quindi perché rotazione spaziale: perché le stelle non fuggono via. Estendendo il concetto, sarebbe anche il perché le Nubi di Magellano non fuggono via, ma anzi mostrano bellissimi fenomeni mareali. Siccome Feynman diceva che se un fenomeno ha almeno tre diverse angolazioni da cui può essere spiegato, con lo stesso risultato, può essere che stiamo facendo scienza, questa che abbiamo appena detto, enormemente la più utile ma anche la più statica, è la prima angolazione da cui abbiamo guardato e cercato di spiegare il fenomeno.
La seconda e la terza angolazione derivano dal tentativo di guardare sempre lo stesso fenomeno ma di cercare di intuirne l’origine. Può essere benissimo che il suo incremento stia scemando, ma questo non esclude che sia stato maggiore in passato. A noi interessa capire se c’è, e poi presupporre che in passato ci sia stato di più (non serve presupporre che continui a crescere, anche se continua a crescere).
L’esempio del grande ascensore galattico a cosa serviva? A cercare di intuire il tipo di moto inerziale: se scopro un effetto tipo/peso (per cui cioè necessito di accelerarmi per misurarlo) alla periferia del grande ascensore, o escludo il moto rettilineo uniforme, o includo materia che non vedo. Il fatto che l’effetto tipo peso sia simmetrico e contrapposto per ogni coppia diametrale di periferie mi dice che mi trovo in moto inerziale, e cioè, avendo escluso il moto rettilineo uniforme, in caduta libera. Il fatto che non abbia una direzione privilegiata ma un senso di rotazione mi suggerisce che si tratta di una marea dello spazio, non degli oggetti, perché lo spazio, non possedendo inerzia, può solo ruotare di più, se mi accorgo che l’inerzia degli oggetti è compensata da qualcosa. Questo non perché mi diverta la cosa, affatto, ma perché al solito altrimenti debbo non solo inserire materia che non vedo, ma farlo in maniera crescente come se piovesse dal cielo, visto che mi sono accorto che sono in moto uniformemente accelerato e l’effetto marea può solo aumentare con il tempo (e questo sia se immagino una situazione di espansione, che una situazione di collasso). Questo non vuol dire che la galassia stia tirando diritto in uno spazio preesistente e infinito. Non sa nulla di tutto ciò. Sta recandosi, con movimenti complicatissimi, verso il punto in cui risulta minore il suo momento d’inerzia, perché questa è la condizione meno dissipativa della sua inarrestabile caduta libera. Ma farebbe questo anche se l’universo fosse in collasso, cioè lo stesso essa si muoverebbe, come componente netta di complicatissime influenze, verso il punto in cui ha più spazio attorno. Che le altre galassie ce la facciano arrivare è tutta un’altra questione, ovviamente, e sarebbe così in ogni caso: il moto è un moto fortemente perturbato dalle irregolarità locali, per cui i vuoti cosmici si ingrandiscono, invece di affollarsi di galassie. Infatti, per stare in una ipotetica stabile condizione di minimo possibile momento d’inerzia, la galassia dovrebbe anche avere spazio che da un certo punto in poi le gira attorno al contrario, in una disposizione resa impossibile da raggiungere per ogni struttura fin dall’origine dell’universo (dall’entropia), pur rimanendo vera a livello globale: così quella ideale è la condizione/disposizione esattamente opposta a quella offerta dai vuoti cosmici, i quali quindi si ingrandiscono, assicurando con la loro altissima entropia che l’irregolarità o disomogeneità locale è una condizione che le galassie non possono superare, pur tendendo globalmente alla massima omogeneità con la loro ricerca del massimo distanziamento reciproco. Credo che con molta probabilità vedremmo pressappoco tutto ciò allo stesso modo anche se l’universo stesse collassando, perché noi vediamo solo il passato dell’universo, ed il passato di un universo in collasso sarebbe molto simile a quello di un universo in espansione.
Il terzo tipo di angolazione da cui guardare lo stesso fenomeno, ma argomentazione sempre che ci fa fare l’elemento marea, è quella più propria dei primi tre esempi dell’articolo, ed è probabilmente quella a cui facevi più riferimento tu. In parte l’articolo è molto chiaro, in parte ho risposto con un po’ di fenomenologia, in parte aggiungo una curiosa osservazione che non ho messo nell’articolo: se riesco ad imprimere una accelerazione radiale alla luna, ma senza toccarla fisicamente, anche il suo giorno comincerebbe a durare meno di un mese, cioè smetterebbe di rivolgere sempre la stessa faccia alla terra. A parte questo, la pertinenza dell’effetto di scematura sta nel gradiente di aumento, non nel fenomeno stesso. Per il resto vale un po’ quello che ho detto finora sulla conservazione della disomogeneità locale e sul motivo di ciò (e sul motivo per cui la rotazione in conseguenza aumenta con il tempo). Più pertinente, cosa che fa di questa una reale terza angolazione, è sempre il motivo per cui supposte rotazioni aggiuntive degli oggetti sfocino invece in rotazioni spaziali: se noti ho detto “accelerare senza toccare la luna”: questo perché non c’è accelerazione radiale senza innesto di inerzia nei sistemi. Per cui siamo sempre lì, o inserisco materia o faccio ruotare lo spazio (come se fosse semplice, vero?).
Come al solito sono andato lungo, per cui mi riprometto di scrivere qualcosa sul concetto di background domani. A presto!
LikeLike
Ho riletto l’esempio di interazione terra-luna e non riesco a conciliare questa frase …
” If we take the Moon away, distancing it from the Earth, the inertia of the bulge, whilst its level falls, gives more angular momentum to the Earth spin, making the day get shorter.”
…con le informazioni che posseggo in proposito.
Sappiamo che la Luna si sta effettivamente allontanando di circa 4 cm/anno dalla Terra. Questo comporta un rallentamento della rotazione terrestre e un conseguente allungamento della durata del giorno terrestre. ( un miliardo e mezzo di anni fa il giorno durava 18 ore)
Tra Marte e Phobos succede esattamente il contrario: Phobos si avvicina a Marte perché l’effetto della protuberanza in quel caso esercita una attrazione retrograda. la velocità di rotazione di Marte cresce nel tempo.
LikeLike
Sì certo Mauri, è come dici tu, ma perché il sistema Terra-Luna sta facendo questo autonomamente, senza accelerazioni di altra natura. Così anche per Phobos, che però è piccolissimo e perde energia gravitazionale più che accelerare la rotazione di Marte. L’ipotesi mia dice invece che se qualche accelerazione esterna (ad esempio l’accelerazione da espansione dell’universo) agisce facendo allontanare i due corpi, non di 4 cm ma cospicuamente, allora il giorno diventerebbe più corto per entrambi, perché l’allontanamento “forzoso” o “arbitrario” avrebbe inserito dell’inerzia dentro i due sistemi. Quindi ad esempio se la Terra e la Luna stessero cadendo dentro un buco nero, per tutto il tempo in cui la caduta non causasse a sua volta nuovi effetti mareali (il che è impossibile, perché l’allontanamento stesso è già un effetto mareale, ma supponendo che non sia così per semplicità), si allontanerebbero fra di loro ruotando più velocemente su se stessi, perché ciò compenserebbe parte dell’energia orbitale persa. Tra un po’ scrivo sulla faccenda del background.
LikeLike
Ah, scusa, rileggendo quello che hai scritto ieri, mi ero scordato un passo: Sì, la somma radiale delle azioni mareali è nulla, la marea è proprio questo. Nel nostro caso la rotazione dello spazio è un nuovo tipo di effetto di marea proprio per questo, perché aggiungendo inerzia remota toglie inerzia propria. La somma è nulla. Questo fatto permette alle strutture di sopravvivere senza spappolarsi in un universo uniforme ad ogni scala, anche la più piccola.
LikeLike
Così vedi.. il dibattito è utile. Preciso meglio e poi passo al background.
Sono nel grande ascensore, precipito in caduta libera verso un centro di massa esterno, traccio la direttrice come dicevamo, non trovo il senso ma pazienza. Cosa sento se mi metto ai due estremi della direttrice? Un peso negativo, cioè un peso verso il bordo e non verso il centro dell’ascensore. Cioè la mia inerzia propria. I due pesi negativi ai due estremi sono esattamente contrapposti, e la somma è perciò nulla.
Sono adesso sempre nel grande ascensore, precipito in caduta libera verso il punto che mi pare il più vuoto possibile al netto di tutte le altre influenze, perché lì il mio ascensore minimizza il suo momento d’inerzia. Facendo questo, come la galassia nella boccia di vetro, l’ascensore ruota di più. Si sta facendo più piccolo? Non ha senso affermare questo perché non avremmo un riferimento esterno all’universo cui compararlo. Cosa sta facendo in effetti?
Pensiamo alla ballerina sul ghiaccio, che, all’opposto di quanto da lei previsto, si sente le braccia più pesanti. Perché? Perché è in caduta libera da un bel po’, e le sue braccia sentono l’effetto divaricativo (mareale) prodotto dalla accelerazione uniforme (inerzia propria: pesano al contrario, verso fuori, e sempre di più). Se ruota di più lei, aggrava l’effetto. Se ruota di più il suo spazio locale, cosa che aggiunge inerzia remota, l’effetto è opposto, e le sue braccia tornano a pesare come prima. Il sempre mutevole (perché dipende dal moto delle altre galassie) punto più vuoto è l’attrattore netto della sua caduta libera fin dall’origine dell’universo. Con questa semplice regola l’universo si è mantenuto allo stesso tempo uniforme a livello globale (tutti gli ascensori tendono a stare lontani) e discreto a livello locale (tutti gli ascensori, seppur con relazioni complicate fra di loro, tendono a rimanere interi), nonché dinamico (nessun ascensore raggiunge mai quell’attrattore netto, tutto quel vuoto che serve a lui ma che vogliono pure gli altri, cambiando continuamente le carte sul tavolo). Quindi se la minimizzazione tendenziale del momento d’inerzia è la causa della rotazione spaziale, quest’ultima è pure il rimedio all’aumento del momento d’inerzia causato dalla caduta libera. Siccome non c’è mai stato un momento in cui la galassia, come ogni cosa, non sia stata in caduta libera, è lecito supporre che la massa, lo spazio, la sua curvatura e il suo spin siano nati assieme.
Andiamo al background. Non so se esistano altre definizioni di background, ma io lo uso in un senso relativistico che può sembrare a volte ambiguo per la sua commistione col concetto di orizzonte, ma non lo è. Prendiamo la nebulosa di gas e polveri (semplifichiamo tutto il più possibile) da cui è nato il sistema solare. Tutti i gas e le polveri insieme determinano una curvatura dello spazio (dello spaziotempo) che poi ciascun atomo o ione o molecola o polvere segue come data. Prendiamo un atomo di riferimento: anche lui ha concorso a creare la curvatura, ma segue il tracciato della sua caduta libera come se la curvatura fosse la forma in sé dello spazio, nel periodo di tempo abbastanza breve in cui non cambia, ovviamente. Anche nell’attimo successivo farà così, pur essendo cambiato qualcosa intanto per via del moto collettivo. La relazione di questo tipo si descrive dicendo che l’effetto della nebulosa di cui l’atomo fa parte è dare un background all’atomo. L’atomo fa parte dell’universo proprio perché e finché ha un background. E’ poi l’esigenza di studio a definire quanto profondo debba essere il background: se c’è una nebulosa vicina, è probabile che la si debba includere nel background per determinare correttamente il moto dell’atomo. Se quella nebulosa vicina fa parte del suo background, anche l’atomo, nel suo piccolissimo, influenzerà la nebulosa. La relatività è un gioco in cui, se giocano gli altri, vuol dire che stai giocando anche tu.
Mercurio è piccolo e molto vicino al Sole, eppure il Sole non determina da solo l’intero background di Mercurio. Se inserisco tutti i pianeti nel background di Mercurio, ho una buonissima definizione del suo background. Il movimento istantaneo di Mercurio segue quello che gli dice il suo background, anche se questo suo movimento sta influenzando cosa il background gli dirà l’istante dopo. Ma questo invece non basta a fare del Sole e di tutti i pianeti un background accurato di Nettuno o di Plutone, dove devo tener conto del concorso di tantissimi oggetti esterni a loro. E il Sole, che è molto grosso in confronto a tutti, è il suo stesso background? Tutt’altro, niente è per se stesso il background. Il suo background sono sì certo tutti gli oggetti del sistema solare, ma solo per una piccola parte. Se voglio capirne il movimento devo approfondire (o sprofondare, verso l’orizzonte) molto il background, ed includere almeno l’intera galassia.
Lo spazio è il tramite di questa relazione, non è nient’altro. Tutta la materia della galassia ne determina la curvatura, così anche la stella più piccola ne viene determinata nel proprio movimento istantaneo, salvo concorrere a determinarla in conseguenza di ciò. Tutta la materia della galassia, facendo ruotare lo spazio locale, assume un peso che impedisce la deformazione centrifuga della propria caduta libera, causata da un peso negativo opposto, così anche la stella più piccola, tramite la rotazione, vede compensato il suo peso negativo, salvo concorrere a determinare la rotazione in conseguenza di ciò.
L’universo nel suo insieme non solo è indipendente dal background, come si dice, ma secondo questa definizione non ha affatto un background, per questo è difficile costruire una relatività universale.
Il background profondo, cioè l’orizzonte, di una galassia, è quello che determina tutto lo spazio di quella galassia, senza che ne serva altro, e la galassia ne viene determinata in tutto il suo movimento netto istantaneo, salvo con questo concorrere a determinarlo. Questo quand’anche il background possa essere considerato in espansione. Per quanto riguarda tutto il movimento istantaneo di una galassia, è il background che si sta espandendo, non lo spazio. La galassia non ha una filosofia dello spazio, ma usa come date le proprietà istantanee che trova, e, salvo concorrere anche lei ovviamente, attende novità per l’istante dopo.
Quindi non l’universo in espansione, ma la galassia che si muove “nello” spazio come se il proprio background fosse in espansione. Non serve altro spazio, poiché anche questa galassia fa da background alle altre.
Quindi l’atomo o il granello di polvere, a seconda della profondità scelta da noi, vede la geometria dello spazio, determinata dal background, come curva, rotante, in espansione. Questo è tutto quanto ne determina il movimento istantaneo, salvo concorrere ed attendere il feedback nell’istante successivo.
LikeLike
Ciao Giorgio, grazie per le ulteriori descrizioni della tua ipotesi. Ti propongo le mie sensazioni dopo averle lette.
Mi sembra che questo tipo di dinamica cosmica sia una vera e propria coreografia in cui ogni passo è determinato fin dall’inizio e porta, in una infinita catena causa-effetto, ad una cascata di configurazioni teoricamente prevedibili o comunque sempre univoche.
Un pensiero identico a questo è quello che, già due secoli fa, era stato espresso chiaramente da Laplace (Saggio sulle probabilità).
Sembra quindi che in uno scenario così squisitamente deterministico i fenomeni quantistici non possano trovare alcuno spazio, pur essendo l’unica realtà a livello microscopico per tutta la materia che costituisce il sistema complesso.
Ora, quando parli di background continuamente mutevole per via delle mutue influenze, sembra di capire che la correzione di rotta avvenga istante dopo istante, sulla base delle interazioni di ciascun ente con tutti gli altri, come composizione istantanea degli effetti prodotti, indipendentemente dalla distanza di chi li produce.
Se questa è la corretta interpretazione significa che a determinare il risultato partecipano anche i corpi al di fuori dell’universo visibile? Ossia la rotazione di una galassia è influenzata “istantaneamente” anche da ciò che non siamo in grado di vedere perché ormai troppo lontano per essere raggiunti dalla sua luce?
Questo significherebbe che siamo in presenza di una sorta di entanglement generalizzato, che evoca, scenari propri dei fenomeni quantistici, in un contesto che abbiamo definito meramente deterministico.
LikeLike
Ciao Mauri.
Secondo me tutta questa faccenda del determinismo è impostata male, non da te personalmente ma da un po’ tutti noi. Non ritengo che l’approccio bottom-up, dal basso verso l’alto, aggiunga indeterminismo all’universo. La QM aggiunge dinamiche probabilistiche ad un contesto altrimenti ferreo, con i vari tipi di conservazione di carica, parità, ecc. che predeterminano il risultato, tant’e vero che si cercano, e si trovano, le nuove particelle facendo la differenza col risultato atteso, in termini di energia, carica, spin ecc. Non aggiunge indeterminismo. E come dicevo nella parte di discussione avvenuta su L’Infinito Teatro, la QM trova tutto lo spazio che vuole (sempre con le sue regole ferree) in un contesto di indifferenza al background. Il processo iterativo istante dopo istante non è altro che il processo di integrazione, essendo l’integrale il nostro metodo matematico per la descrizione di un percorso: fanno così sia la relatività che la QM, col suo integrale dei percorsi. Può essere che io abbia reso male il concetto, ma è difficile descrivere il background in altri termini. Come accennavo, Feynman diceva che il percorso di una particella fra A e B è stato ipotizzato come descrivibile in base a tre possibili criteri: il percorso più breve, il percorso più economico (meno dissipativo), il percorso più probabile. Ebbene, diceva, abbiamo scoperto che la particella fa tutte e tre le cose insieme. In sostanza, se rileggi i miei ragionamenti, faccio così anch’io: rispetto a che cosa una galassia fa il percorso più breve, quello meno dissipativo e quello più probabile? Rispetto al suo background, come fa anche un asteroide o un granello di polvere. E’ in questo senso che diciamo che il background determina il percorso della galassia.
Questo è determinismo in che senso? Se immaginiamo due che si stanno scrivendo in una galassia dall’altra parte dell’universo, mentre vedono noi molto “spostati verso il rosso” (probabilmente perché abbiamo bevuto molto vino), si stanno lamentando dell’opposto, cioè che noi sembriamo determinare loro. Il background è un concetto relativistico. Nulla ci dice cosa fanno la galassia ed il suo background se guardati insieme: poiché l’universo, come dicevo, non ha background, l’universo non è determinato da nulla. Purtroppo non abbiamo ancora costruito un fast ticking point da cui immaginare di guardarlo, proprio perché non abbiamo superato questo scoglio alla nostra immaginazione.
La mia prospettiva basata sull’osservatore concreto può sembrare troppo semplice, o semplicistica, o deludente, perché non mette cose che non vede (materia oscura, energia oscura, inflazione) in posti che non conosce. Però, appunto, è più semplice. Molto più semplice.
Quando si cerca di quantizzare lo spazio da che punto di vista si sta guardando l’universo? O meglio, si tratta propriamente di un punto di vista? Che ruolo si prende l’osservatore, o si dà all’osservatore? Come dicevo a mio fratello piccolo, è come se io guardassi da casa in TV una partita di tennis: siamo a Wimbledon, e la telecamera momentaneamente sta zoomando la pallina sull’erba. Siccome l’immagine sta ampliando il campo, e comincio a vedere Federer, poi il campo, poi a mano mano il pubblico, poi lo stadio, poi gente per strada che sta passando in bici per caso ecc., ebbene cosa mi si dice? Che la telecamera sta “semplicemente” aumentando il numero dei pixel del mio televisore, e che la partita è preregistrata. Questo è il risultato di uno sguardo matematico senza osservatore concreto. Questo è il vero determinismo Mauri. Io cerco di capire come l’universo possa funzionare, non come possa autoimitarsi in un modello matematico come un film circolare e sempre esistente. Cioè l’osservatore per me non è uno spettatore che conosce abbastanza matematica da interpretare cosa sta dietro un videogioco. Così come un modello semplice e che funziona con meno speculazioni non è necessariamente deterministico, e sicuramente non è deterministico in quel senso, perché nessuno ha preregistrato un film, il tempo non ha affatto questo senso, e l’universo non è a sua volta condizionato da nulla.
Ad ogni modo: le leggi di Keplero non sono state accettate perché qualcuno si è fatto un giro fino ai confini del sistema solare ed ha controllato che le cose andassero proprio così, ma perché erano enormemente più semplici della teoria degli epicicli di Tolomeo. La materia oscura sembra costretta a stare in posti molto strani, e seguire quindi la stessa logica degli epicicli. Da lì eravamo partiti.
Quanto al discorso entanglement: probabilmente, come nel caso dell’integrazione del percorso, ad un certo punto, nel tentativo di costruire una relatività universale, troveremo non proprio un entanglement, ma qualcosa che gli somiglia molto. Insomma un equivalente relativistico. L’entanglement quantistico ha bisogno di tre punti, cioè un osservatore e due punti remoti in una certa relazione tra loro. Già la considerazione dei sistemi spazio-rotanti richiede tre punti, uno proprio, uno remoto ed uno fast ticking immaginario. Quando troveremo (costruiremo) un quarto punto (vedremo (?) con quali caratteristiche), a seconda se esso può o non può sostituire il punto fast ticking, avremo o no qualcosa che somiglia ad un entanglement relativistico.
A tal proposito, tanto per lanciare un tema di riflessione e non per aprire un dibattito che rischierebbe di essere infinito (ma su cui mi piacerebbe, quando il professore starà bene, proprio parlarne in privato con lui): la galassia di Andromeda, come si sa, sta a 2.000.000 di anni luce da noi. Siamo così lontani che la nostra galassia e Andromeda, con buonissima approssimazione, si stanno muovendo reciprocamente con velocità costante: allora la nostra galassia, dal punto di vista gravitazionale (cioè per regolarsi su dove andare) “vede” Andromeda dov’è ora o dov’era due milioni di anni fa? E chi crede che lo spazio sia quantizzato, come risponde a questa domanda?
LikeLike
Ciao Giorgio, Keplero è stato un grande, indubbiamente, ma le sue leggi sono puramente descrittive, non forniscono spiegazioni. Solo con Newton abbiamo avuto il passaggio decisivo, da una narrazione di ciò che appare, alla spiegazione , comunque locale e circoscritta entro i limiti classici, delle cause.
Una cosa è prevedere con buona approssimazione la posizione futura dei pianeti, un’altra è elaborare una teoria, un modello generale che conduca a quel risultato come conseguenza dinamica e non puramente cinematica.
Pensando ad un esempio molto concreto, nella scienza delle costruzioni, l’assetto reale di una struttura iperstatica è determinato dal gioco di equilibrio e congruenza. Le sole equazioni che determinano la statica della struttura non sono sufficienti a dare una risposta univoca, offrono infinite soluzioni, dato che esistono infinite configurazioni staticamente equilibrate grazie alla presenza dei vincoli. Il problema da un punto di vista statico è indeterminato.
La soluzione di questi sistemi richiede , oltre alle equazioni della statica che attengono all’equilibrio del corpo, anche la definizione dello stato di deformazione e spostamento, in modo da selezionare la soluzione che sia al tempo stesso “equilibrata e congruente” , rispetti cioè le condizioni di congruenza relative alla continuità materiale della struttura e delle condizioni cinematiche dettate dalla presenza dei vincoli.
Ecco quindi che non è sorprendente il fatto che nella realtà un percorso goda di più proprietà concomitanti e confluenti , quello di essere il più breve, il più veloce, il più economico.
Ma se questi sono i rilievi “narrativi” che possiamo fare, resta aperto il discorso sulle cause che rendono veloce, breve ed economico, quell’assetto.
La cicloide è una curva molto popolare nel nostro Teatro: ne abbiamo parlato più volte mettendo in luce le sue proprietà di evoluta, tautocrona, brachistocrona descrivendo queste caratteristiche che trovano riscontro non solo geometrico, ma anche fisico. Non solo la forma, descrivibile come pura costruzione geometrica, ma anche l’essenza dinamica, causa delle proprietà esibite fisicamente.
La tua domanda finale, su Andromeda è proprio la stessa che ponevo, nel commento precedente, chiedendomi se l’azione gravitazionale, nel modello “caduta libera”, si sviluppa istantaneamente o alla velocità della luce. Da quanto ho capito le onde gravitazionali si propagano alla velocità della luce e questa non è più solo una ipotesi , ma una realtà misurata dai rilevatori Ligo e Virgo, nonché dal satellite Fermi.
Così la risposta ingenua potrebbe essere semplicemente che ciò che otticamente vediamo è coevo di ciò che gravitazionalmente sentiamo.
Il lento avvicinamento tra le due galassie (100 Km/s ?) richiederà quattro o cinque miliardi di anni per giungere alla collisione, anche di più, tenendo conto della presenza del terzo incomodo, M33 che cadrà nel frattempo su Andromeda. Se in questo momento dovessi calcolare la loro attrazione reciproca, metterei al denominatore il quadrato della distanza a cui Andromeda si trovava quando ha emesso la luce che vedo ora. Ma certo Enzo potrebbe darti una risposta più elaborata e soddisfacente della mia, speriamo presto, appena si sarà ripreso dalla operazione che incombe.
LikeLike
Non mi sento proprio, da quante cose ho scritto, di essere uno che non parla continuamente di cause, ma so che se c’è una certa probabilità che quello che vado dicendo interessi qualcuno è per la sua semplicità.
Se intendi che non spiego la causa del perché tutti i corpi ci appaiono in caduta libera, interpella una fonte di certo più autorevole di me: il nostro grande Albert, che su questa intuizione (esattamente sul fatto di cadere senza sentire il proprio peso) ci costruì la sua teoria della gravità. Non sono io a dover spiegare perché non pongo limiti di scala a questo concetto, ma chi li pone, ovviamente – oltre a dire a quale livello li pone ed il vero motivo per cui li pone -. Io posso solo aggiungere che i corpi seguono lo stato in cui si sentono senza peso per i motivi che individuava Feynman.
Ho certo introdotto la novità di trattare con un qualche approfondimento in più il concetto di inerzia. Se l’inerzia propria non è compensata da qualcosa, il corpo non altera la propria condizione di caduta libera (cioè preferirà sempre la traiettoria che non gli fa sentire il proprio peso) ma il senso di percorrenza della direzione della caduta libera (il senso indeterminabile della direzione di caduta del nostro ascensore), in quanto la sua caduta passa da una condizione di caduta libera gravitazionale a una di caduta libera inerziale (in senso stretto sono tutt’e due inerziali, per cui comincerò a indicarle come g-inerziale (gravità) e p-inerziale (propria). Per un osservatore remoto può sembrare una situazione in cui operi una antigravità, ma in realtà non è così, il corpo sta solo seguendo la traiettoria che non gli fa sentire il proprio peso, esattamente come nel caso tradizionale. Quando si trova in caduta libera inerziale (nel senso stretto in cui qui uso questo termine, p-inerziale) l’ascensore percepirà pur sempre maree direzionali sotto l’influenza di centri di massa vicini, ma privilegerà la direzione data dalla loro componente netta, percorrendola in senso opposto a quello che ci aspetteremmo. Contemporaneamente, non essendo un corpo rigido, conoscerà un nuovo tipo di marea, che si oppone all’aumento dell’inerzia propria delle sue componenti durante la caduta libera (accelerazione uniforme = deviazione delle geodetiche o delle traiettorie di ciascun componente). Questo aumento dell’inerzia propria avviene in senso radiale, ed è compensato quindi dalla crescente rotazione locale dello spazio che aggiunge inerzia remota in senso radiale in modo che l’ascensore possa continuare a sentirsi senza peso, esattamente come nel caso iniziale, sia nel suo complesso che nelle sue componenti. Perché la massa collettiva riesce a far ruotare lo spazio? Per lo stesso motivo per cui riesce a curvarlo. Se gli effetti di marea di una cometa che precipita su Giove prevalgono facendola a pezzi senza che lo spazio locale della cometa tenti di compensare ciò, è perché la cometa e Giove sono spazialmente comoventi fra di loro, cioè fanno parte di un’unica rotazione rispetto al centro di una galassia stabilizzata.
La caduta dell’ascensore terminerebbe (“p-centro di massa”) nel momento in cui l’ascensore si trovasse in una zona caratterizzata da una remota rotazione spaziale uniforme e contraria disposta attorno alla propria (se cioè fosse al centro della sua “boccia”), ma questa situazione è altamente improbabile che possa verificarsi in modo stabile a causa dell’entropia universale, e lo sarà sempre di più. Quindi lo stesso principio spiega sia la grande omogeneità a grandissima scala, sia la grande disomogeneità a piccola scala, in un contesto perdurante e conservativo delle strutture.
Per fornire un’ulteriore analogia, ho accennato al caso del fotone, che non ha inerzia propria (infatti non accelera), non ha massa a riposo (infatti non decelera in presenza di gravità) ma ha inerzia remota (anche se in questo caso massa relativistica, ma l’equivalenza è piena, la massa relativistica è un tipo di inerzia remota), per cui può arrivare “in ritardo” se deflesso da una grande massa, rispetto alla condizione in cui la grande massa non ci sia e possa arrivare fino al medesimo osservatore facendo un percorso diritto, pur non avendo in nulla modificato la sua velocità in senso proprio, ma compiendo semplicemente, se visto dall’osservatore, un percorso più lungo – e pagando in redshift la perdita di energia (equivalente alla massa relativistica corrispondente) -.
Non ho risposto di proposito e ho lanciato di proposito invece la domanda su Andromeda, hai inteso molto correttamente Mauri. Le onde gravitazionali sono emesse dai corpi accelerati, oppure ruotanti in difetto di equidistribuzione lungo il piano di rotazione. Infatti ho premesso: il moto è in gran parte assimilabile ad un moto rettilineo uniforme. Ebbene, la componente del moto che è rettilinea e uniforme non fa emettere ad Andromeda onde gravitazionali; solo la componente accelerata lo fa. Quindi ti assicuro, la domanda è una bella domanda, ed io non ho una soluzione in tasca così semplice da apparire anche logica.
https://en.wikipedia.org/wiki/Speed_of_gravity
LikeLike
Ah, dimenticavo. Perché l’inerzia propria se non è compensata provoca tutto ciò? Perché l’Universo vive nel tempo, acquistando, dal punto di vista di una galassia-osservatrice, continuamente massa relativistica, cioè inerzia remota. Siccome la massa relativistica (a differenza di quella gravitazionale) è relativa, questo è equivalente a dire che la galassia è sempre più accelerata, cioè ha crescente inerzia propria, e nessun esperimento è in grado di distinguere le due cose (perché sono la stessa cosa).
Ora, io penso che chi invece dice “materia oscura”, “energia oscura” o “inflazione” non sta dicendo cause, ma parole, nel senso che ogni volta dovrebbe dire: “apparente bisogno di” e poi aggiungere uno dei componenti oscuri o la componente reliquia.
LikeLike
Ciao Giorgio, per qualche giorno non mi farò sentire a causa di vari impegni e trasferimenti, ma intendo ripercorrere le molte cose che hai descritto nei tuoi interventi per meglio comprendere la tua idea.
Buon weekend, e cerca di dormire un po’ ogni tanto ( visti gli orari dei tuoi commenti)
LikeLike
Hai ragione Maurizio!! E’ il Teatro-Cosmo ad essere così appassionante, probabilmente, e il nostro sforzo di comprensione è una forma di dolce ed intrigante corteggiamento che ci toglie il sonno.
Buon weekend.
LikeLike
Caro Giorgio, riprendo il dialogo dove lo avevamo lasciato.
L’ipotesi su cui stai lavorando è che l’universo è costituito da infinite entità locali, in caduta libera , che si allontanano reciprocamente una dall’altra sempre più rapidamente, anzi con accelerazione crescente. Questa dinamica è dettata semplicemente dalla configurazione dei percorsi di minima azione che sono veri e propri “binari” su cui transitano tutti gli attori, Non sono binari statici ma, proprio a causa della evoluzione delle posizioni assunte da ciascuno, si modellano e rimodellano continuamente. Questo implica anche una evoluzione univoca di tutti i fenomeni in una infinita rete di catene causa-effetto.
Continuo a descrivere qualitativamente quanto penso di avere compreso ( magari non è proprio quello che tu intendevi).
Materia ed energia oscura sono espedienti introdotti per rendere conto di apparenze che non trovano un riscontro con i calcoli basati sui modelli di cui disponiamo, risolvono qualche problema ma ne creano altri, prima di tutto la dimostrazione della loro stessa reale esistenza ( oscura).
Se il modello basato sulla caduta libera riesce a giustificare quelle rotazioni troppo veloci delle galassie, senza mettere in crisi altre osservazioni, resta comunque la necessità di trasferire questa visione qualitativa in una forma matematica che consenta anche una verifica quantitativa.
Credo che se la tua ipotesi venisse sottoposta ad una valutazione di referee per la pubblicazione questa richiesta di formalizzazione emergerebbe.
Ora, non ho idea di come si possa strutturare una metrica di un caduta libera universale, ma è qualcosa su cui sarebbe opportuno fare un pensiero. Magari è un sentiero che hai già intrapreso.
Ci sentiamo…
LikeLike
Rieccomi! Grazie Maurizio spero tutto ok.
1/n
Vorrei riannodare il filo logico del discorso.
Sono partito in origine dalla constatazione che il rinvenimento di qualsiasi forma di materia oscura non avrebbe risolto il problema originario per cui la si cerca, cioè il problema della rotazione delle galassie. Infatti la dinamica delle fusioni passate non avrebbe potuto mantenere la materia oscura nella posizione in cui la si desidera mettere, in modo da evitare picchi inevitabili nella rotazione delle stelle al centro della galassia. In più la luminosità delle galassie è strettamente correlata alla velocità di rotazione (legge di Tully-Fisher), il che richiede che l’eventuale materia oscura deve marcare proprio strettamente la materia barionica, seguendola pedissequamente come il gregge segue il suo pastore. Inoltre la preponderanza gravitazionale della materia oscura (nella posizione richiesta, oltre gli aloni) predice l’esistenza di troppe galassie nane (rispetto a quelle osservate), ed una distribuzione più uniforme delle galassie satelliti, rispetto a quella osservata (che predilige abbastanza il piano galattico del fratello maggiore). Ma, se un’eventuale rinvenimento della materia oscura non risolve i nostri problemi, dobbiamo correggere la nostra legge della gravità? La relatività? Le varie teorie MoND non sono riuscite nel proposito, perché la loro predittività si è dimostrata non solo non conclusiva, ma addirittura controproducente (per loro). Quello che ho notato è che tutti coloro che pretendevano di correggere la GR facevano e fanno questo discorso: “la stella vicina la bordo delle galassia va troppo veloce? Ebbene, questo vuol dire che ha meno inerzia che gravità”. Questa cosa può venire in mente soltanto se non si è compreso a sufficienza cos’è l’inerzia: non soltanto la resistenza di un corpo ad essere accelerato, ma pure la resistenza di un corpo ad essere decelerato. Se un corpo sentisse più gravità che inerzia, a parte tutte le modifiche alla sua stessa forma, ed accelerasse per guadagnare inerzia, aggraverebbe il problema. Non sarebbe più in caduta libera e quindi uniformemente accelerato, e quella che descriverebbe non sarebbe un’orbita.
La mia soluzione rivede il ruolo dell’inerzia, non tocca la GR, e rende il principio di equivalenza, da presupposto indimostrato che era, una proprietà emergente ed unitaria del funzionamento dell’Universo.
Queste considerazioni sono il motivo vero della mia teoria. Quando mi si è invitato a indicare le cause della esistenza di grandi sistemi (interconnessi) spazio-rotanti, ho cercato di farlo, ma forse dovevo marcare di più l’accento sul fatto che ciò che fondamentalmente cambia qui è la visione dell’inerzia, che invito a valutare, per la connessione logica dell’inerzia remota con la massa relativistica (che ne diventa una tipologia), e per la comprensione più unitaria del redshift fra componente velocità e massa, o in alternativa accelerazione propria. Gustare anche, perché ciò è profondamente relativistico, e sembra legare tutti i punti di vista possibili in questo nostro universo, insegnando loro a vedersi sempre più simili e rispettivi.
Ma, andando alle cause diciamo più tecniche, ho proposto il discorso mareale: noto un’accelerazione relativa, compensata in ciascun punto; non è esattamente come la marea, ma sembra avere la stessa caratteristica di base: lascia il corpo interessato senza un “peso netto” in nessuna direzione, libero dall’influenza di alcuna forza, come anche la marea fa (perché è una forza apparente, ma io direi meglio, relativa).
Nell’esempio del grande ascensore, la possibilità di indagare la direzione, ma non il senso, ci dice che è al lavoro il principio di equivalenza. Un’altro fenomeno assimilabile alla marea dovrei avvertire dentro quell’ascensore, interessante questa volta il piano ortogonale alla direzione da me tracciata, cioè la pressione verso l’esterno causata dalla divergenza delle geodetiche. Questa pressione è esattamente ortogonale, e di nuovo i vettori “peso” si compensano fra di loro, come nelle maree. Tuttavia, anche se riuscissi a rilevare il fenomeno, nemmeno adesso riuscirei a stabilire il senso della traiettoria. Potrebbe farlo un osservatore esterno, ma io no. Il piano attorno a cui il fenomeno è massimo, contrariamente a quanto si potrebbe pensare, non è nemmeno leggermente spostato in avanti, verso il senso di caduta. Questo perché il moto di caduta libera è inerziale, mentre se quel piano fosse spostato in avanti genererebbe un peso netto. Tuttavia, abbiamo visto, la rotazione dello spazio dell’ascensore neutralizza esattamente ogni effetto di questa marea crescente. Per me anzi, che sono dentro, questo tipo di rotazione non è rilevabile, non genera nessuna forza centrifuga ma anzi compensa ogni accelerazione centrifuga. Posso rilevarla solo facendo calcoli complicati e attraverso il redshift, ma a condizione, per vederlo, di abbandonare la mia solidarietà inerziale con l’ascensore per un po’. Mi accorgo che questa componente rotazionale è potente, mentre la componente mareale tradizionale, quella che mi ha fatto tracciare la direzione, è niente al confronto. Questo mi dice che l’ascensore è in caduta da un bel po’, mentre nessuna meta è provvisoriamente alle viste.
Continuo domani perché è tardi.
Ho scoperto che non ho modo di inserire formule, mi manca qualcosa come invece c’è nell’Infinito Teatro. Se qualcuno sa aiutarmi mi fa un piacere. A domani.
LikeLike
Ciao, rieccomi. Ti ringrazio intanto per l’interessamento per la questione delle formule, proverò da domani.
2/3
Un ultimo accenno alla questione del’inerzia. L’ultimo che tentò di andare oltre alla concezione newtoniana dell’inerzia (senza peraltro riuscirci, se non come aspirazione) è stato Mach. Diceva: se un corpo fosse l’unico nell’Universo, non avrebbe inerzia, perché non ci sarebbe qualcosa rispetto a cui misurarla, o semplicemente rispetto a cui muoversi o ruotare o meno. Einstein amava tantissimo questa visione, senza peraltro poter purtroppo concludere nulla in questo senso, perché morì in un periodo in cui ancora la questione del moto delle stelle, date le ridotte possibilità di misura sistematica del redshift di stelle di altre galassie, e le idee ancora limitate sulla reale forma e dimensione in 3D della Via Lattea, e ancora più limitate sulla sua massa, era una questione che sembrava secondaria, irrilevante. La relatività così non è una teoria machiana, e non ha una concezione autonoma dell’inerzia. L’introduzione dei concetti di inerzia propria e di inerzia remota è però, allo stesso tempo, pienamente machiana e pienamente relativista. Quindi non infinite unità locali, ma moltissime unità intimamente correlate, e PER QUESTO in caduta libera. La singola unità locale è in caduta libera proprio perché è correlata con tutto. La metrica necessaria non disegnerà, qualora trovata e convincente, la logica della dispersione universale, ma la logica della tenuta universale di numerosissime unità locali in caduta libera, proprio in conseguenza dell’esistenza di tutte le altre. Una necessità sia intrinseca che estrinseca perciò, dettata dalle due forme dell’inerzia, pienamente correlate e relative (inerzia propria e inerzia remota). La galassia è fatta di centinaia di miliardi di oggetti, tutti in caduta libera, ma la rotazione li tiene insieme da miliardi di anni. Questo è il lavoro di fine tuning di una logica che desidererei trasmettere e che è sia relativistica che machiana. L’Universo non ruota, perché non avrebbe qualcosa rispetto a cui ruotare (quindi la galassia ruota perché ha tutte le altre galassie rispetto a cui ruotare..! Il loro spin netto -di tutte!- è l’opposto del suo; e questo vale per ogni galassia). Se l’Universo non ruota, probabilmente l’espansione è il fattore intrinseco che lo tiene insieme, cioè lo stesso fine tuning ribaltato a livello universale.
Tu mi dirai: “ma in che epoca vale il principio di Mach, ora o nel passato?”. Ed hai ragione a chiederlo!
Guardiamo la galassia di Andromeda. La vediamo un po’ di taglio, ma ne ammiriamo senz’altro la meravigliosa struttura a spirale. E’ un po’ più grande della nostra. Ora, guardiamo alle sue stelle più esterne, diciamo un anello posto a 60.000 anni luce di raggio dal suo centro galattico. Se questo anello di stelle sta vedendo (o vedeva all’epoca) il suo centro di rotazione o di massa dove era 60.000 anni prima, e relativamente alla distanza, così tutte le sue stelle in mezzo, credi tu che Andromeda possa mai presentare, in una qualsiasi epoca, la struttura che noi vediamo in foto? E se il suo buco nero centrale, il suo centro di massa, sta vedendo le stelle che gli stanno tutte INTORNO dove erano decine di migliaia di anni prima, mentre si sta muovendo, come componente netta, verso un punto dietro l’ammasso della Vergine a centinaia di km al secondo, in che senso è il loro centro di massa e noi lo vediamo starci in mezzo? Tu dirai: “anche le altre lo stanno facendo”. Certo, ma lui dovrebbe vederle dove e quando lo facevano decine di migliaia di anni prima.
Due considerazioni. Intanto, possiamo semplicemente dire che non c’è verso di risolvere questo problema quantizzando lo spazio. I loop sono ingegnosi lavoratori, ma ognuno coi suoi vicini, e basta..! Come i pixel del mio tv, se devono lavorare tutti assieme, possono solo trasmettere qualcosa di fatto altrove, non qualcosa che stanno facendo loro stessi da protagonisti, perché altrimenti in questo caso ognuno starebbe solo interessando il suo vicino. Ora, la mia visione ti può sembrare atomista o parcellizzata, ma non coincide con questa.
Seconda considerazione. A che mi serve che l’espansione metrica dello spazio indotta dalla energia oscura risolva concettualmente il problema dell’orizzonte cosmologico, se non mi consegna una metrica che risolva il paradosso di Andromeda che ho sotto il naso? Come per la materia oscura, abbiamo trovato un concetto che non ci serve per risolvere il problema principale (la metrica ad ogni scala) e che invece produce anche un bel problema, come vedremo domani.
LikeLike
Dunque, rieccoci.
3/3
In merito all’espansione metrica dello spazio causata dall’energia oscura, si è costretti a ricorrere, nel caso della luce, a quel discorso circa l’espansione “nello” spazio prossima e espansione “dello” spazio remota che tanto stupore desta quando applicato alla materia e segnatamente, dati i nostri argomenti, alle galassie. Ricordate? La mia tesi era che ogni punto proprio può espandersi soltanto (o essere accelerato uniformemente o “cadere” senza peso) “nello” spazio, mentre esso vede che il suo background si espande “con” lo spazio (per quello che può significare: la portata di questa affermazione è solo evocativa, significa che non si presuppone uno spazio infinito newtoniano da riempire – ma questo è già implicito nella nostra concezione di universo, anzi propriamente l’Universo non ha un ulteriore background rispetto a cui espandersi -). Ebbene: nel caso dell’espansione dettata dall’energia oscura, si è costretti a concedere questo lusso alla luce. La luce, si dice, in ogni “proprio” intorno sta continuando a viaggiare alla velocità c (rispetto all’intorno stesso), ma sia lo spazio che ha già superato che quello ancora da superare si stanno espandendo metricamente, cosicché al suo arrivo nel nostro telescopio il fotone sembra aver percorso lo spazio che effettivamente (quando? oggi?) ci separa dalla galassia o quasar di origine ad una velocità maggiore di quella della luce. Fin qui niente da ridire, dal punto di vista meramente formale. Il problema è il bilancio energetico. Dunque: se la nostra galassia è “ferma” (dal punto di vista dell’espansione, ovviamente) non succede nulla alla sua energia cinetica; l’aumento di spazio, e quindi di potenziale gravitazionale, dovrebbe essere compensato dalla densità dell’energia oscura (non lo è, ma pazienza). Il fotone arriva però con una lunghezza d’onda maggiore, il che significa con meno energia. Rapida carrellata: un fotone in uno spazio piatto non perde energia, fino a quando almeno non incontra qualcosa che gliela faccia perdere (e che quindi la possa assorbire in una qualche forma); quando un fotone risale invece il pozzo gravitazionale, non perde velocità come la materia, ma perde comunque energia per il lavoro compiuto, attraverso appunto il redshift. Nel mio modello di espansione, il fotone perde energia, e manifesta quindi un redshift, in maniera equivalente per i seguenti motivi correlati e relativi: o per la massa relativistica remota, o per l’accelerazione mia propria. Ma nel mondo dell’energia oscura, mentre si può intuire perché ha allungato la sua onda, però perché perde energia? Sia che si voglia dare un significato gravitazionale che antigravitazionale all’energia oscura, mediamente lui ne ha trovata metà dietro e metà davanti; lo stesso col potenziale del nuovo spazio. Sean Carroll, fisico e divulgatore di successo, molto impegnato contro le bestialità varie di coloro che propongono modifiche alla GR, ma anche molto impegnato nella difesa del modello standard, ha ammesso (non certo nei libri, ma nelle profondità di Twitter): “mi dispiace, ma dobbiamo ammetterlo, l’energia non si conserva”. Dico io: ma siamo sicuri che ci serve questa energia oscura? Non ci fa conservare né la densità, né, cosa molto molto più stupefacente e compromettente, l’energia. Non è un problema che ci stiamo portando a casa questo? Da noi si dice: facciamo come uno che si mette i ceci nelle scarpe.
A questo punto volevo parlare un po’ di energia del vuoto, ma rimandiamo.
Ho appena capito, seguendo il consiglio nella tua ultima mail Maurizio, che qui il blog senza upgrade non mi fa inserire immagini di sorta.
Ovviamente ci torneremo, anche perché devo fare delle osservazioni.
Per chi avesse una raffinatezza matematica migliore della mia, che è inadeguata, invece due spunti. Il primo sarebbe la derivazione a complemento della deviazione delle geodetiche (nel senso che sommando le due funzioni, la deviazione risulterebbe sterilizzata, per cui si può ricavare quanto cercato per “differenza”). Il secondo, la derivazione dalla meravigliosa geometria delle spirali, nel senso ad esempio dello sviluppo della rotazione di un oggetto in moto rettilineo uniforme dal punto di vista proprio, che parte dal centro lungo un qualsiasi raggio sul piano galattico, intendendo quindi il suo moto come studio della rotazione della tangente o derivata lungo ogni punto della spirale.
LikeLike
Ciao Giorgio, innanzi tutto provo una idea, per le formule e le immagini. Ho scritto una formula e un po’ di testo. Poi ho fatto lo screenshot e ritagliato la parte che volevo. Ho caricato la jpg sul sito
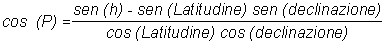
Postimage https://postimages.org/it/ dopo essermi registrato gratuitamente.
Dopo il download hai a disposizione varie possibilità, tra cui ho scelto la seconda (link diretto).
Qui si dovrebbe vedere la formula e i commenti…
Si potrebbero provare anche le altre opzioni. La comodità sarebbe di poter avere la formula sempre visibile su parte dello schermo e su un’altra parte leggerne la descrizione che ne dai sul post.
Può sembrare complicato ma dopo la prima volta è facilissimo.
Venendo ai contenuti che hai aggiunto ci devo meditare sopra. E’ inevitabile che il discorso si vada complicando, quando si passa alla rappresentazione matematica, in particolare con la ricerca di luoghi di punti, come accenni nelle ultime righe.
Per il momento posso dire di essermi fermato ad una comprensione generale della tua idea, ma per andare più in profondità dovrei recuperare molte cose sepolte sotto la polvere di oltre mezzo secolo, quando mangiavo a colazione tensori e Hamiltoniane, roba ora indigesta.
Se l’energia , come dice Carrol, “non si conserva” spiace anche a me. Era una cosa che mi ero abituato a pensare e la trovavo confortevole e rassicurante. Ma ormai sono più di cento anni che nella fisica e nella matematica ci siamo abituati a vedere crollare certezze e simmetrie. Ci adegueremo.
LikeLike
Piccolo errore di nome nella jpg ….. Ho richiamato un filename FORMULA invece di FORMULE..

LikeLike
grandioso Maurizio!! Grazie!!
Cercherò di riprodurre stasera quanto hai fatto tu, ma intanto sono veramente contento. Quella della spirale è una idea affascinante, e non ha bisogno di hamiltoniane. So che più di qualcuno sul sito ha le competenze giuste ed il gusto per queste tipo di visione geometrica, perché in passato, quando avevo più tempo, ho letto cose fantastiche e stimolanti. Io ci starei dei mesi a recuperare questo gap.
Quando al principio di conservazione dell’energia, a tutto si può rinunciare, certo, ma farlo per un motivo oscuro e probabilmente inutile è un po’ più duro. Non pensate che dovremmo dare alla faccenda un sapore più concludente?
Mi rifaccio vivo appena ho più tempo, riscrivo meglio l’integrale, dico qualcosa dal sapore meno aleatorio sul sigma, aggiungo qualche idea sulla geometria a spirale che immagino, e spero di aggiungere qualcosa al dibattito. Grazie intanto!
LikeLike
ok.. non così splendida ancora ma il tuo suggerimento funziona alla grande Mauri! Tutto consiste adesso nell’avere una migliore qualità del jpg. Mi è sufficiente per scrivere il nuovo articolo, intanto.
Mi rimane da rispondere su due grosse questioni, il determinismo e la metrica. Il primo argomento è da affrontare con il giusto relax, ed avremo modo di farlo certamente in maniera serena nel futuro. Il secondo richiede, per essere affrontato per intero, tanti piccoli passi. Se il prossimo articolo “mi esce” come lo sto immaginando, questo sarà un primo piccolo passo.
Intanto tengo a mente la nostra amica mirabilis: il mio problema era avere una equazione che valesse indipendentemente dalla massa, da un punto di vista dimensionale, e mi ero quindi cacciato nel forzare il moto rettilineo uniforme. In sostanza però guardavo da un’altra parte: stavo trascurando che “the same tracking” del primo articolo è quella forza che divisa per qualsiasi massa (o meglio, densità di massa) mi dà l’accelerazione uniforme di cui vado cianciando continuamente a proposito di caduta libera. Per questo la mirabilis è perfetta e rende inutile e fuorviante la mia formulazione precedente.
Ciao, ancora grazie, a presto.
LikeLike
ovviamente non si tratta di una spedizione di Amazon.. intendevo “the same traction” non “the same tracking”. Vicissitudini. Anche se non è affatto detto che l’Universo non lasci le sue tracce, come Pollicino.. 🙂
LikeLike
Bene, Giorgio , aspetto il prossimo passo.
Quanto a Pollicino… L’esempio calza, il compito però è più ambizioso. Non si tratta solo di individuare le briciole, ma capire come era fatta la pagnotta.
Ciao!
LikeLike
🙂
Uno è stato fatto col mio nuovo articolo, in italiano
https://giorgiomistenda.com/2019/03/30/la-calma-di-andromeda-e-lo-sforzo-di-charlie/
A presto, ciao buon fine settimana.
LikeLike
Finalmente, come avevo promesso, qualcosa che ha sapore un po’ più di pagnotta 🙂 :
https://giorgiomistenda.com/2019/04/01/il-centro-della-galassia-una-holostar/
Non sono riuscito ad utilizzare quel metodo per le espressioni, evidentemente ciò che si può fare nei commenti non lo lasciano fare negli articoli (mi spuntava sempre e solamente il link).
Comunque la grafia, benché orribile, dovrebbe essere comprensibile. Dovrò arrendermi e coi lacrimoni fare l’upgrade.
Giudico il punto a cui sono arrivato interessante.
LikeLike
Ciao Giorgio, ho letto ambedue i nuovi articoli ma mi riprometto di rivederli con più calma, per coglierne meglio tutti i contenuti. Comunque un lavoro notevole e che penso ti abbia dato soddisfazione.
Peccato per l’upgrade, ma non mi viene in mente che altro si potrebbe fare per farne a meno, se non scrivere solo le premesse iniziali dell’articolo e poi aggiungere un commento in cui si prosegue nei dettagli, scrivendo le eventuali formule ( in pratica il primo commento sarebbe proprio l’articolo stesso).
Grazie per avere citato il nostro scambio di opinioni, ma il mio contributo è stato solo di provocare le tue ulteriori riflessioni, niente di più.
LikeLike
Maurizio, il discorso della spirale logaritmica è stato decisivo. E sono sicuro che la competenza matematica tua e del prof mi sarebbero utilissime. Ho capito bene il discorso della tangente costante, ma devo studiare meglio la evoluta e la involuta per avere alcune risposte. Ad esempio: la tangente ruota alla stessa velocità ω dell’angolo yOx? E altre cose. Comunque se questa proporzione che ho scoperto in seno alla Via Lattea ha senso, è già di per sé qualcosa di elettrizzante.
Intanto siamo vicini per quanto riguarda Sgr A*:
https://tech.everyeye.it/notizie/10-aprile-eso-pubblicare-foto-storia-buco-nero-371237.html
Per quanto riguarda l’upgrade, è obbligatorio per un anno, e costa una bella cifra. Mi girano un po’.
LikeLike
Giorgio, la velocità della materia in movimento lungo i bracci della spirale dovrebbe essere molto diversificata e irregolare.
Esiste anche una galassia in cui la rotazione avviene addirittura in due sensi opposti:
https://www.vialattea.net/content/4249/
Insomma, mentre la geometria , la cinematica, è quella della spirale, da un punto di vista dinamico la complessità è molto maggiore. Ti segnalo anche questo link sulla nostra galassia, in cui descrive un moto di ondeggiamento del piano di rotazione: https://www.repubblica.it/scienze/2013/11/03/news/la_strana_danza_della_via_lattea_nei_dintorni_del_sole-69667878/
Per l’upgrade aspetta, prova prima a strutturare l’articolo con un breve abstract introduttivo e mettere tutto il resto nel primo commento , dichiarando esplicitamente che si tratta dell’articolo dettagliato.
Alla fine, per chi legge, non cambia molto rispetto ad avere il testo integrato.
LikeLike
Ciao Maurizio. Grazie per le osservazioni.
Il problema della rotazione dello spazio, se è questa la soluzione, è un tipico problema cinematico, per definizione. Infatti preciso che è indipendente dalla massa del corpo che usiamo come “tracciante”, immaginandolo proprio “muoversi” in un contesto piatto, con densità della materia attorno bassa, diffusa e costante. Tutto il resto è dinamica, e per l’esattezza dinamica gravitazionale, dettata dalle variazioni di densità come tutti le conosciamo.
L’apparente bisogno di materia oscura è costantemente attaccato e proporzionale alla quantità di materia barionica, e noi stiamo cercando proprio una relazione cinematica che lo risolva, mentre la dinamica gravitazionale è già risolta dalla GR.
Mentre noi, necessariamente, guardiamo la curva in coordinate polari, il punto di origine O ha come unico riferimento il segmento OP, di cui conosciamo già la dinamica: per lui si muove di moto rettilineo e uniformemente accelerato, in caduta libera, ed indifferentemente nei due sensi (prima dinamica); è il sistema di coordinate x,y che, per il punto O, ruota in senso opposto in maniera costante (seconda dinamica): come in ogni caduta libera, P segue la via più breve, la linea retta, ma lo spazio nel frattempo ruota; P poi segue le distorsioni gravitazionali della distribuzione di densità (terza dinamica): anche in questo caso tende a seguire la linea retta, ma di fatto descrive una geodetica, che è il percorso più breve in caduta libera in uno spazio curvo (non è indifferente nei due sensi). Noi qui stiamo definendo e collegando le prime due dinamiche (di per sé piuttosto semplici), e descrivendo una soluzione puramente cinematica, come la richiede l’ipotesi di una rotazione dello spazio. Non lo facciamo perché abbiamo bisogno di farlo, ma perché quello che osserviamo causa l’apparente bisogno di qualcosa che già sappiamo non poter risolvere il problema. Sulla dinamica effettiva invece, cioè sul motivo, ci siamo già dilungati sulla caduta libera della galassia, sull’ascensore e sulla marea, il che implica, siamo o no d’accordo su questo, che non deriva da un fattore endogeno alla galassia.
Conosco le oscillazioni delle stelle sul piano galattico, ma queste oscillazioni non hanno indotto nessuno a dire qualcosa sulla materia oscura, e per un motivo ben chiaro: perché non c’entrano (non conosciamo il passato di fusioni della nostra galassia). Quanto alla galassia che ruota in due sensi: nessuno ha detto che in seguito ad una fusione lo spin spaziale risulti conservato. Anzi anche senza fusione, le Nubi di Magellano non sembrano averne più uno autonomo. Per ognuno di questi fatti, se immagini di introdurre la materia oscura, aggravi il problema piuttosto che risolverlo.
Considerando α=1 per tutta la zona popolata di stelle della galassia, b si riduce (p nell’articolo) a 1/e per un angolo tangente di circa 69,8°, perché, da quello che ho capito finora, l’angolo sarebbe uguale a arctan(e).. (se ho capito bene). Considerando l’angolo effettivo, per la nostra galassia circa 78°, la proporzione di influenza gravitazionale sarebbe all’incirca pari alla proporzione fra materia normale e materia oscura, come ho scritto finora.
Infatti se noi consideriamo il complemento a 90° dell’angolo effettivo, quello che gli inglesi chiamano pich, circa 12°, allora abbiamo che con una proporzione di materia normale pari al 14,5% (DM=85,5%) siamo ancora nei range di stima.
LikeLike
Intanto ho trovato questi due studi:
https://arxiv.org/abs/astro-ph/0605728
https://arxiv.org/abs/astro-ph/0005241
Il primo dà come “pitch” medio 23,50°, il secondo 17,25°. La media bruta è 20,38°. Per 20,20° p è l’inverso del numero di Nepero. Per gli amanti delle simmetrie questo è qualcosa di incredibile, se ci pensi: r = se^(1/e)αθ con α=1⁄γ≅1. Ciao.
LikeLiked by 1 person